Salut,
Pour la question 1) (et c'est à peu prés la même chose pour les autres), tout dépend de ce que tu as comme théorèmes dans ton cours :
En fait, toute les limites avec des log et des puissances et où x tend vers 0 ou bien +oo peuvent se déduire de l'unique résultat
}{x}\!=\!0)
, mais ça demande un peu d'astuce pour arriver à systématiquement se ramener à ce cas là donc ça oblige les étudiants à être... un minimum astucieux...
Donc assez souvent (mais pas toujours), on rajoute dans le cours d'autre résultats concernant limites en 0 et +oo des log et puissance, par exemple le résultat bien plus général suivant :
Si

et

sont deux réels avec

alors
\big)^\alpha}{x^\beta}\!=\!0\ \ \text{et}\ \ \lim_{x\to 0^+} x^\beta \big(-\ln(x)\big)^\alpha\!\!=0)
Si ce dernier résultat est dans ton cours, alors le 1) est une application directe.
Sinon, si tu n'as que le résultat "de base", ben... il faut être astucieux...
Avec les x qui n'est "que" au carré au dénominateur, ça ne suffit pas pour "manger" les log du numérateur qui lui est au cube. Donc il faudrait augmenter l'exposant du numérateur et ça se fait très facilement via un changement de variable, en prenant par exemple
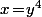
(
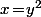
ça suffirait, mais c'est pour montrer le principe) :
\big)^3}{x^2}<br />=\lim_{y\to\infty}\dfrac{\big(\ln(y^4)\big)^3}{(y^4)^2}<br />=\lim_{y\to\infty}\dfrac{\big(4\ln(y)\big)^3}{y^8}<br />=\lim_{y\to\infty}\dfrac{4^3}{y^5}\bigg(\dfrac{\ln(y)}{y}\bigg)^3=\dfrac{4^3}{\infty^5}\!\times\!0^3=0\!\times\!0=0)
