Je ne parviens pas à montrer que la covariance empirique de deux variables définit un produit scalaire sur
Ainsi je ne montre pas que la forme est définie...
Merci de votre aide !
Covariance et produit scalaire
4 messages
- Page 1 sur 1
Covariance et produit scalaire
par jeje56 » 21 Oct 2021, 15:41
Bonjour à tous,
Je ne parviens pas à montrer que la covariance empirique de deux variables définit un produit scalaire sur
.
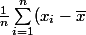(x_i-\bar x)=0 \Leftrightarrow \forall i,x_i=\bar x)
Ainsi je ne montre pas que la forme est définie...
Merci de votre aide !
Je ne parviens pas à montrer que la covariance empirique de deux variables définit un produit scalaire sur
Ainsi je ne montre pas que la forme est définie...
Merci de votre aide !
Re: Covariance et produit scalaire
par tournesol » 21 Oct 2021, 21:48
Un carré étant toujours positif , une somme de carrés est nulle ssi chaque carré est nul .
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :