Matrice de covariance - indépendance

[MacManus]

Bonjour !

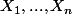
Soient n variables aléatoires réelles définies sur l'espace probabilisé , indépendantes et suivant toutes la loi normale centrée réduite N(0,1) de densité .
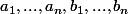
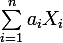
Soient des réels. On considère les variables aléatoire Y et Z définies par Y= et Z=

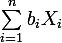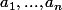
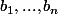
1) Calculer la matrice de covariance du vecteur (Y,Z). A quelle condition portant sur les vecteurs a=() et b=() cette matrice est-elle inversible ?

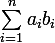
2) Montrer que les variables aléatoires Y et Z sont indépendantes ssi =0


Merci pour votre aide.

[kazeriahm]

Bonjour,

qu'as tu réussi à faire ? Sais-tu former la matrice de covariance d'un couple de v-a ?

[MacManus]

eh bien je sais bien quelle "tête" de la matrice dans le cas d'une seule variable aléatoire mais pas dans le cas d'un couple. La matrice est définie par si i j et si i=j. Mais cette définition est bien pour une seule V.A non ?

[kazeriahm]

Bah non, on parle de matrice de covariance de taille n dans le cas de n variables aléatoires, ici tu en as 2 : Y et Z. Applique la définition dont tu m'as parlé

[kazeriahm]

Dans ta définition tu parles de la matrice de covariance du vecteur , là tu dois calculer la matrice de covariance de

[MacManus]

d'accord on doit avoir dans ce cas la matrice de covariance suivante : .

[kazeriahm]

voila, donc maintenant faut calculer chacun des termes, en écrivant les définitions de Y et Z, etc... le calcul est pas compliqué si on a pas peur des notations

[MacManus]

Salut. Je peut réécrire cette matrice sous la forme :

c'est bien ça? Ou encore :

[kazeriahm]

voila, et tu peux calculer var(X_i) et cov(X_i,X_j)

[MacManus]

Puisque les V.A. X_1,...,X_n sont indépendantes, on peut écrire que
cov(X_i,X_j)=0 normalement

[kazeriahm]

oui, si i different de j, que se passe-t-il quand i=j ?

[MacManus]

oui cov(X_i,X_j)=0 si i différent de j et dans le cas où i=j, on a cov(X_i,X_i)=var(X_i). Mais je ne vois pas bien comment calculer Var(X_i) même si je connais la définition...

[kazeriahm]

ca veut dire quoi que X_i suit une loi N(0,1) ?

[MacManus]

ah ok oui Var(X_i)=1^2=1
On obtient enfin :

[kazeriahm]

Voila

vois-tu comment repondre aux questions posees maintenant ?

[MacManus]

Eh bien en calculant le déterminant de cette matrice , on doit avoir :

[kazeriahm]

Oui, tu noteras que le determinant de cette matrice est toujours positif (matrice de covariance = matrice symetrique positive). En poussant un peu, comment exprimer grace a une inegalite tres celebre que le determinant de ta matrice est nulle ?

[MacManus]

Oui on utilise l'inégalité de Cauchy-Schwarz. Mais dans le cas d'égalité (pour cette inégalité), celà revient à dire que les vecteurs a et b sont colinéaires

[MacManus]

Bonsoir!

j‘aimerais revenir sur la question 2 du post #1

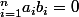
L'implication de gauche à droite est "simple" (Y et Z indépendants implique cov(Y,Z) = , mais pour la réciproque, ne s'applique-t-elle pas dans le cas de vecteurs gaussiens ? comment procéder ?

merci par avance pour votre coup de main