Courbe polaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Nov 2009, 20:26
par Zweig » 08 Nov 2009, 20:26
Salut,
Je dois déterminer les points doubles de

, avec

Je suis donc amené à résoudre : \rho(\theta) = \rho(\theta)
Ce qui me donne

Normalement (d'après correction), je devrais trouver

, mais je ne comprends pas trop la correction : déjà pourquoi ils ajoutent de l'exponentielle à

? Ensuite, j'comprends pas trop d'où ils sortent la dernière équation pour déterminer
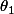
:
http://moduloserge.free.fr/HX1-07/DM/dm04_courbes_corr.pdfMerci d'avance.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 08 Nov 2009, 20:54
par Skullkid » 08 Nov 2009, 20:54
Salut, les points doubles sont obtenus pour
 = \vec{OM}(\theta'))
, soit en complexe
 e^{i\theta} = \rho(\theta') e^{i\theta'})
. Tu peux avoir
= \rho(\theta'))
sans avoir de point double (sur un cercle, par exemple).
Et tu peux même avoir des points doubles avec
 = - \rho(\theta))
, comme dans ton cas !
-
mathelot
 par mathelot » 08 Nov 2009, 21:12
par mathelot » 08 Nov 2009, 21:12
bonsoir,
il semble que l'image
)
soit l'affixe d'un point M du plan
que l'on écrit (quasiment) sous forme trigo
=(1+tan(\theta))e^{i \theta})
on en déduit:
si

ou

=\theta\\<br />\rho(M)=1+tan(\theta)\\)
sinon
=\theta+ \pi\\<br />\rho(M)=-(1+tan(\theta))\\)
car

je ne sais si cela répond à la question.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Nov 2009, 21:49
par Ericovitchi » 08 Nov 2009, 21:49
Ce qui est sûr c'est qu'il semble bien y avoir un point double :

-
mathelot
 par mathelot » 08 Nov 2009, 22:35
par mathelot » 08 Nov 2009, 22:35
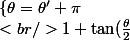=-(1+\tan(\frac{\theta'}{2})))
utiliser
=\sqrt{2}-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités