Transformer une équation cartésienne en courbe polaire ?

[fransgilles]

Bonjour à tous,

Je cherche comment transformer une courbe en coordonnées cartésiennes en une courbe en coordonnées polaires, à savoir:

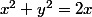
a) en

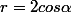
ainsi que

b ) en

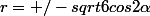
Le but de l'exercice étant de calculer l'aire intérieure à la courbe a) et extérieure à la courbe b)

Merci beaucoup pour votre aide, bonne journée et bonne année!

[chan79]

Salut
remplace x par

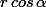
et y par

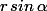
le premier est un cercle
le second une lemniscate de Bernoulli

[fransgilles]

Salut
remplace x par

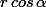
et y par

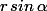
le premier est un cercle
le second une lemniscate de Bernoulli

merci pour ces précisions Chan,

donc si j'ai bien compris, pour transformer n'importe quelle courbe en coordonnée polaire, on pose:







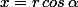
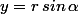
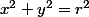
avec:


?

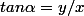
[chan79]

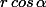
tu remplaces x par et y par
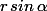
x²+y²=2x





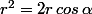
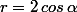
x²+y²=2x peut s'écrire (x-1)²+y²=1 c'est le cercle de centre I(1;0) et de rayon 1

r=OM



on retrouve l'équation polaire en écrivant que

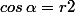
[Sylviel]

Oui pour passer de cartésienne en polaire c'est toujours facile : il suffit de remplacer x par rcos(a) et y par r sin(a). L'autre sens est parfois un peu plus délicat.