Courbe polaire

[Anonyme]

Salut,
Quelle est la méthode la plus simple pour étudier la courbe polaire p(theta)=cos(theta)+sin(2theta) svp? Il me semble qu'il faut se servir de p(pi-theta)=-p(theta).
Je vous remercie à l'avance de vos réponses.

[le_gabe]

p(x) = cos(x) + sin(2x)

on sait que sin(2x) = 2sin(x)cos(x) donc:

p(x) = cos(x) + 2sin(x)cos(x)
p(x) = cos(x)[1 + 2sin(x)] voilà une autre forme...

Après tu dois faire quoi???
Df = |R

p(x) = 0 ?
si cos(x)=0 -> x = pi/2 [modulo]
si 1 + 2sin(x) = 0 -> sin(x)=-1/2 -> x =-pi/6 ou 7pi/6 [modulo]

p'(x) = -sin(x) + 2cos(2x)
les zéros, le signe croissant décroissant etc...

J'éspère que j'ai pu t'aider...
:++:

[le_gabe]

Au fait pourquoi polaire??? Cette fonction t'as glaçé le sang...looll
En fait elle a pas grand chose de polaire...
On a du mal se comprendre
une équation polaire proche de l'équation que tu m'as donnée serait:

r = cos(phi) + sin(2phi) par exemple

Mais ça veut plus du tout dire la même chose que tu m'as écrit en premier à ce moment là!!!

[Anonyme]

Merci d'avoir répondu si vite! Seulement... c pas la fonction x->cosx + sin2x qui me pose problème mais bien l'équation polaire r=cos(phi) + sin(2phi)
:-|. Au fait quel est le problème dans l'expression que j'ai donnée? (l'équation polaire p(theta)=cos(theta)+sin(2theta) peut effectivement s'écrire r=cos(phi)+sin(2phi) mais je vois pas la différence) ;P @++

[Anonyme]

De toutes facons r est variable donc on peut écrire r(phi).... non?

[Anonyme]

tu sais la gabe je t'emmerde

[Anonyme]

tu n'ai qu'un aliboron et tu connais rien en math et pourtant tu ose répondre à ma question.
va chier connard. tête de bite. tu m'as fait haîr les maths avec tes saloperies de démonstrations. va te faire enculer.

[Galt]

Une remarque en passant : ce n'est pas en insultant les autres membres que tu auras des réponses à tes questions.
Chacun fait ce qu'il peut, et personne n'est obligé de répondre

[tristan]

tu n'ai qu'un aliboron

Un modo pourrait-il m'expliquer ce qu'est un "aliboron" avant de supprimer la discussion ?

[Anonyme]

tu sais la gabe je t'emmerde

Petite info: c'est pas moi qui ai écrit ce message j'ai aucune raison d'insulter quiconque, y a quelqu'un que ca semble amuser de se faire passer pour moi... enfin ca m'apprendra à poster un message sans m'être identifié.

[Anonyme]

D'ailleurs ca me parait complètement invraissemblable qu'une personne en insulte une autre juste après l'avoir remerciée et alors qu'elle n'a toujours pas trouvé de solution à son problème.

[Galt]

Ok, alors j'explique
Etudier une courbe en polaire, ce n'est pas forcément étudier les variations de r, on se contente souvent d'étudier son signe et les diverses symétries
Ici
Si on change en 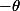, il n'y a rien de bon, mais si on change en on trouve . On étudie la courbe sur , puis on fait une symétrie par rapport à l'axe des abscisses
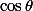s'annule en et en , en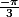
La courbe va donc passer 3 fois par l'origine (+ 1 par symétrie) , avec les 4 tangentes mentionnées.
En r vaut 0, on est en O, avec une tangente verticale. De à 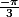r est négatif, donc on est au dessus de l'axe des abscisses, côté x négatif. En 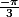r s'annule, nouveau passage à l'origine, avec tangente 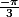, puis r passe positif, donc on est en dessous de l'axe des abscisses jusqu'à r=0
En 0, r vaut 1, on passe au dessus de l'axe des abscisses, et r s'annule en
Reste à faire la symétrie.
Le calcul de r' servira pour déterminer les tangentes, mais c'est moins utile.

[Anonyme]

Merci beaucoup! euhm je crois que 1+2sin(theta) s'annule en 7pi/6 et en 11pi/6. Sinon si on tient à passer par la dérivée de r (r'(x)=-4sin²x-sinx+2), comment étudier son signe sur I=[0,2pi] stp? Il doit falloir étudier le signe du polynôme -4X²-X+2, dont les racines sont X1=(racine(33)-1)/8 et X2=(-racine(33)-1)/8. Il existe 2 valeurs a et b de x dans I telles que sinx=X1 et 2 valeurs c et d de x dans I telles que sinx=X2. Donc r'(x)=0<=>x=a ou x=b ou x=c ou x=d. Mais comment en déduire le signe de r'(x) sur I arf je m'embrouille... @+ et merci encore

[Galt]

Oups
Oui, c'est en que s'annule.
Je regrette
J'insiste sur un point : on ne se sert pas de la dérivée en général pour les courbes en polaire

[Anonyme]

Mais comment connaître de manière assez précise le tracé d'une courbe polaire r en étudiant que le signe de r(x)? Par exemple si on sait que r(x)>=0 sur un intervalle [a,b], comment tracer r sur [a,b]? (r(x) peut a priori prendre n'importe quelle valeur positive pour x dans [a,b], par exemple 100 000 000)

[Anonyme]

oh... l'expression d'une courbe polaire est bornée bien sûr... désolé. Enfin il n'empêche que r(x) peut prendre n'importe quelle valeur comprise dans un certain intervalle

[Anonyme]

quoique non une courbe polaire est pas forcément bornée enfin là c'est le cas