Cosinus hyperbolique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nico742
- Membre Naturel
- Messages: 47
- Enregistré le: 03 Oct 2007, 17:26
-
 par nico742 » 07 Sep 2008, 12:10
par nico742 » 07 Sep 2008, 12:10
Bonjour, j'ai un autre soucis...
Calculer Cn =
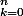
ch(a+bk)
avec (a,b)

R² , n

N
Je vois absolument pas par ou commencer....merci d'avance pour l'aide
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 07 Sep 2008, 12:21
par Quidam » 07 Sep 2008, 12:21
nico742 a écrit:Bonjour, j'ai un autre soucis...
Calculer Cn =
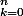
ch(a+bk)
avec (a,b)

R² , n

N
Je vois absolument pas par ou commencer....merci d'avance pour l'aide
Ben si tu partais de la définition de ch(x) :
=\frac{e^x+e^{-x}}{2})
?
-
bobdu67
- Membre Relatif
- Messages: 107
- Enregistré le: 05 Sep 2008, 21:17
-
 par bobdu67 » 07 Sep 2008, 12:26
par bobdu67 » 07 Sep 2008, 12:26
ben tu sait que ch(x)=(e(x)+e(-x))/2
pour n=0 tu a ch(a+kb)= (e(a)+e(-a))/2
pour n=1 ch(a+kb)= (e(a)+(e-a))/2 + (e(a+b)+e-(a+b))/2 (tu simplifie)
puis n=2
tu regarde se que sa donne, et tu essais de trouver une récurence
-
bobdu67
- Membre Relatif
- Messages: 107
- Enregistré le: 05 Sep 2008, 21:17
-
 par bobdu67 » 07 Sep 2008, 12:40
par bobdu67 » 07 Sep 2008, 12:40
donc moi j'ai trouver une truc du genre
somme ch(a+kb)= [e(a)(1+e(b)+e(2b)+...+e(kb))+e(-a)(1+e(-b)+e(-2b)+...+e(-kb))]/2
or tu sait que 1+a+a²+...+a^k=(1-a^(k+1))/(1-a)
donc tu pourra trouver une simplification si je n'ai pas fait d'erreur
 par busard_des_roseaux » 07 Sep 2008, 13:21
par busard_des_roseaux » 07 Sep 2008, 13:21
Quidam a écrit:Ben si tu partais de la définition de ch(x) :
=\frac{e^x+e^{-x}}{2})
?
grâce à cette formule, c_n est combinaison linéaire de deux sommes de progression géométrique de raison

et
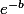
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités