Corps des classes résiduelles

[Archytas]

Salut,
Je voudrais savoir la définition de "corps des classes résiduelles". Je n'ai pas trouvé de réponses convenables sur google ou assez précise pour comprendre la phrase :

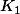
Le corps des classes résiduelles est un espace vectoriel d2 dimension 2 sur , une base étant formée de 1 et de = classe de x vérifiant donc .

Merci d'avance,
Ciao

[Robot]

Quelle est la phrase d'avant ?

Je parierais bien que ça parle de .

[Archytas]

Quelle est la phrase d'avant ?

Je parierais bien que ça parle de .

Il n'y a pas de phrase avant, c'est la première et le titre de la sous partie est "le polynôme x²+x+1 est irreductible sur Z/2Z". Merci pour la réponse rapide, ça a l'air cohérent, c'est bizarre comme nom, mais après tout je sais pas quel petit nom j'aurais donné à ce corps à la place de l'auteur ^^.
Bonne soirée !

[Robot]

Les classes résiduelles, c'est les classes des polynômes modulo X^2+X+1.

Ce qui est bizarre, c'est qu'on ne sait pas que ces classes forment un corps tant qu'on n'a pas montré que X^2+X+1 est irréductible.

[Archytas]

Autre chose si tu as une minute, je vois pas trop à quoi ressemble la cloture algébrique de corps comme Z/pZ etc... j'ai lu sur internet qu'un corps fini ne peut être algébriquement clos et plus on étend les corps (avec les classes d'équivalence quotient comme tu l'as écris) et plus c'est fouillis dans ma tête, les histoires de classes de classes de classes etc...
Si t'as un exemple assez bateau de clôture algébrique d'un corps fini par exemple avec Z/2Z c'est méga top.
Merci,
Ciao !

[Archytas]

Les classes résiduelles, c'est les classes des polynômes modulo X^2+X+1.

Ce qui est bizarre, c'est qu'on ne sait pas que ces classes forment un corps tant qu'on n'a pas montré que X^2+X+1 est irréductible.

C'est assez évident qu'il l'est, comme il est de degré 2 et qu'il n'a pas de racine ^^, non ?

[MouLou]

C'est assez évident qu'il l'est, comme il est de degré 2 et qu'il n'a pas de racine ^^, non ?

Je crois qu'il veut dire que c'est bizarre de parler du corps résiduel, puis de dire que c polynome est irreductible.

[Robot]

D'accord que ce n'est pas dur, mais encore faut-il le dire !

[Archytas]

D'accord que ce n'est pas dur, mais encore faut-il le dire !

Exact ^^ c'est un article d'une revue assez balaise (enfin pour moi) ça s'appelle Quadrature si vous connaissez, j'adore ces magasines . Enfin c'est peut être pour ça que dans un élan de snobisme ou à force d'avoir des lecteurs balaises que le gars a pas jugé utile de le dire !
Désolé je n'ai pas compris MouLou, je ne sais pas ce que c'est qu'un corps résiduel :/.
Merci pour votre aide en tout cas, je vais bosser le sujet un peu cette aprèm je poserai probablement d'autres questions :].
Ciao !!

[Archytas]

Me revoilà,
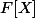
Je voudrais savoir comment on définit précisément les racines de tous les polynômes irréductibles disons de avec F un corps non algébriquement clos. Enfin je vois bien que pour UN polynôme f irréductible minimal on fait et on obtient une bestiole étrange formée de classes d'équivalences. Puis la magie opère on transpose X et on lui donne comme joli nom , une racine est née (enfin autant de racines sont nées que le degré de f si je ne me trompe pas ?!). Mais je ne comprends pas comment on peut parler de l'ensemble de toutes les racines des polynômes irréductibles. Etant donnée la construction je ne vois pas comment les comparer dans un cadre général. Par exemple si on prend F=Q les rationnels et qu'on prend les racines sont bien i et -i pour f et 2i et -2i pour g. Mais si on les défini par classes d'équivalences comme plus haut comment peut on les comparer ?? Comment peut on dire que 2i = 2*i ? Je sais pas si vous me comprenez, c'est un peu confus...
Je demande tout ça parce que dans mon cours le début d'une démonstration de la propriété comme quoi un corps admet toujours une clôture algébrique on pose A={racines de tous les polynômes irréductibles dans F} et je ne vois pas comment cet ensemble est créé. Vous voyez un peu ou non ?
Merci d'avance,
Ciao !

[Robot]

Tu soulèves un point un peu délicat. Apparemment, comme il s'agit d'un article de vulgarisation, la construction de la clôture algébrique est faite un peu en agitant les mains.
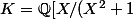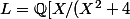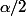
Pour reprendre ton exemple avec les corps et , on peut comparer leurs éléments par un isomorphisme de -algèbres de sur . Le problème est qu'il y a deux tels isomorphismes. Si j'appelle la classe de dans et celle de dans , on peut envoyer sur mais aussi sur .

[Archytas]

D'accord, et ça changerait quoi qu'on choisisse l'un ou l'autre ? Envoyer i sur -a/2 est possible ???? Et c'est toujours possible dans un cadre plus vaste ? Avec F quelconque ? Quelle "réalité mathématique" a a+b avec a et b deux racines de deux polynômes irréguliers différents ? Parce que pour nommer la clôture algébrique de F "corps" il faut déjà pouvoir sommer ses éléments. Dans F=Q c'est pas violent d'étendre sur Q, on le conçoit car on ne rajoute en gros qu'une racine en faisant Q(i) (je sais que c'est pas la clôture algébrique mais bon) mais quand il s'agit de rajouter tous les algébriques c'est un peu le bordel quand on s'y prend avec les classes :/

[Archytas]

Par curiosité, les algébriques ils sont dénombrables ou bien ils ont la taille de R ? De nez je dirai dénombrable mais je suis pas sûr...

[Robot]

Pour voir une construction d'une clôture algébrique, tu peux regarder ici

Oui, l'ensemble des nombres algébriques sur est dénombrable (puisque l'ensemble des polynômes irréductibles sur est dénombrable).

[Doraki]

Tu peux représenter un nombre algébrique x par la donnée de son polynôme minimal et d'une approximation rationnelle de x (dans Q(i)) (suffisemment bonne pour, par exemple, être dans le bassin d'attraction de x par la méthode de Newton)

Construire un polynôme qui annule x+y ou x*y connaissant les polynômes minimaux de x et de y c'est "pas très dur", mais après il faut pouvoir le factoriser en facteurs irréductibles pour trouver lequel est le bon.

Mais bon ça reste assez compliqué.

[Archytas]

Ok merci ! C'est plus clair sans être tout à fait top ^^ mais c'est un début

[Archytas]

Vous auriez un exemple de deux corps k, K tels que K n'est pas une extension normale de k dans sa clôture algébrique ? Je trouve pas d'exemple --'

[Doraki]

k = Z/2Z(X²) et K = Z/2Z(X) ?

[Doraki]

k = Q et K = Q(2^1/3) ?

[Archytas]

k = Q et K = Q(2^1/3) ?

:id: :+++: merci !