Corps contenant Fp

par **simplet** » 20 Oct 2006, 17:48

Bonjour,
on cherche ici à montré que si un polynome P admet une racine dans un corps à p^2 éléments contenant Fp (=Z/pZ) p premier, alors il admet un facteur de degré =< 2.

Tout est en place sauf le point suivant:
" Pourquoi existe-t-il toujours un corps à p^2 éléments contenant Fp??"

Mon prof n'a donné comme simple explication: "cela résulte du fait qu'il y a toujours un polynome irréductible de degré 2 sur Q"...

mais.. pourquoi cela je vous pris?? Avec l'existence de ce polynome je saurais conclure... en appelant Q ce polynome on pose K=Fp[X]/(Q) qui est un corps contenant f(Fp) qui est en bijection avec Fp, où f est la surjection canonique.

merciii

par **Imod** » 20 Oct 2006, 18:16

Je ne suis pas sûr de comprendre ton problème , tu doutes de l'existence d'un polynôme de degré 2 irréductible sur

? Il suffit de considérer

.

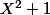
Imod

par **simplet** » 20 Oct 2006, 18:40

Q n'est pas de cardinal p^2...

par **Imod** » 20 Oct 2006, 18:49

Qu'appelles-tu Q exactement ?

Imod

par **abcd22** » 20 Oct 2006, 18:50

Bonsoir,
C'est un polynôme irréductible de degré sur Fp qu'il faut, il suffit de choisir

qui n'est pas un carré et de prendre le polynôme X² - a. Si p = 2 tous les éléments de F2 sont des carrés, mais on peut prendre X² + X + 1, qui est irréductible puisqu'il n'a pas de racine dans F2.

par **Imod** » 20 Oct 2006, 19:00

D'accord , je m'étais un peu perdu dans les notations .

Imod

par **simplet** » 20 Oct 2006, 19:21

oui mais en restant dans le cadre général avec p premier quelconque (c ca ki m'interrsse :-)

par **abcd22** » 20 Oct 2006, 19:29

La réponse que j'ai faite est pour p premier quelconque, il y a juste un cas particulier si p = 2.

par **simplet** » 20 Oct 2006, 19:53

abcd22 a écrit: il suffit de choisir qui n'est pas un carré et de prendre le polynôme X² - a.

Comment est-on sur de son existence? (désolé si j'insiste, mais montrer des "existences" ce n'est pas mon fort :-)

par **yos** » 20 Oct 2006, 20:02

simplet a écrit:Comment est-on sur de son existence? (désolé si j'insiste, mais montrer des "existences" ce n'est pas mon fort

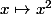
est un morphisme de groupe multiplicatif ayant un noyau non trivial {-1,1} dés que p différent de 2. (Donc pas surjectif non plus car ensemble fini).

par **simplet** » 22 Oct 2006, 08:43

en fait c'est la surjectivité qui nous interesse ici; il existe un a dans Fp tel qu'il n'existe pas de a' vérifiant a'^2=a... ok

merci et bon dimanche

Corps contenant Fp

corps contenant Fp

Qui est en ligne