Optimisation linéaire, plus petit triangle contenant n points
10 messages
- Page 1 sur 1
salut
beaucoup d'indices qui n'aident pas vraiment ...
ensuite considère-t-on que les points sur les côtés appartiennent au triangle ou non ? je suppose que oui et donc des inégalités larges dans la suite ...
je considérerais le triangle équilatéral OAB avec O(0, 0), A(a, 0) et)
donc on a un triangle équilatéral de côté a
on cherche les points M(x, y) à coordonnées entières (je suppose) tels que
0 = (1 - \sqrt 3 )x \le 0[/TEX]
il faut ensuite l'équation de la droite (AB) ... et écrire en core une fois qu'on a x=< y
....
beaucoup d'indices qui n'aident pas vraiment ...
ensuite considère-t-on que les points sur les côtés appartiennent au triangle ou non ? je suppose que oui et donc des inégalités larges dans la suite ...
je considérerais le triangle équilatéral OAB avec O(0, 0), A(a, 0) et
donc on a un triangle équilatéral de côté a
on cherche les points M(x, y) à coordonnées entières (je suppose) tels que
0 = (1 - \sqrt 3 )x \le 0[/TEX]
il faut ensuite l'équation de la droite (AB) ... et écrire en core une fois qu'on a x=< y
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Tu es assez mal parti.
Il convient de minimiser une fonction (linéaire) adéquate de avec des contraintes correspondant au fait que tous les points donnés sont contenus dans le triangle déterminé par
avec des contraintes correspondant au fait que tous les points donnés sont contenus dans le triangle déterminé par  .
.
Edit : j'ajoute que je ne vois pas trop l'intérêt de formuler ça comme un problème de programmation linéaire !
Il convient de minimiser une fonction (linéaire) adéquate de
Edit : j'ajoute que je ne vois pas trop l'intérêt de formuler ça comme un problème de programmation linéaire !
Robot a écrit:Tu es assez mal parti.
Il convient de minimiser une fonction (linéaire) adéquate deavec des contraintes correspondant au fait que tous les points donnés sont contenus dans le triangle déterminé par
.
Edit : j'ajoute que je ne vois pas trop l'intérêt de formuler ça comme un problème de programmation linéaire !
Bonjour,
Merci de répondre aussi vite. J'avais bien compris l'idée générale de l'exercice. Par contre ça ne m'éclair pas beaucoup puisque je je reviens à ma question.
En gros, par exemple, si je donne n=5 points tels que, au hasard, (3,3) (3,4) (4,4) (5,5) et (2,5) sont les points donnés, comment se présenterai mon programme linéaire ?
Pour tester, j'utiliserai Matlab.
Merci encore pour votre réponse
PS: Il existe un problème du plus petit cercle contenant n points, cad un problème similaire à celui-ci mais ici on utilise un triangle équilatéral. La méthode utilisée d'après la littérature et Wikipédia est la programmation linéaire. Le fait que l'on utilise la programmation linéaire pour résoudre notre problème est donc justifiable, et puis ça fait aussi un bon exercice. Il n'est pas forcément nécessaire d'avoir un intérêt. Je suis d'accord que la programmation non-linéaire serait plus simple, il suffirait de minimiser l'aire du triangle équilatéral mais ici je galère... s'agirait-il de minimiser le périmètre ? Cad
zygomatique a écrit:salut
beaucoup d'indices qui n'aident pas vraiment ...
ensuite considère-t-on que les points sur les côtés appartiennent au triangle ou non ? je suppose que oui et donc des inégalités larges dans la suite ...
je considérerais le triangle équilatéral OAB avec O(0, 0), A(a, 0) et
donc on a un triangle équilatéral de côté a
on cherche les points M(x, y) à coordonnées entières (je suppose) tels que
0 = (1 - \sqrt 3 )x \le 0[/TEX]
il faut ensuite l'équation de la droite (AB) ... et écrire en core une fois qu'on a x=< y
....
Bonjour, tout d'abord merci de votre réponse, je crois comprendre l'idée derrière votre méthode. Par contre je crains que vous ayez mal compris le problème. Nous ne cherchons pas le nombre de points à mettre dans un triangle mais plutôt le triangle le plus petit possible contenant n points (qui sont déjà donnés) via une méthode de programmation linéaire. J'ai besoin de connaitre les contraintes, la fonction à minimiser. La variable dont il faut trouver les valeurs est le côté du triangle. ça peut / doit être un vecteur colonne et c'est pour ça qu'il faut s'aider de
Merci encore pour votre réponse
CongEjz9 a écrit:puisque c'est un triangle équilatéral n'est-ce pas ?
Absolument pas ! Le fait que ce soit un triangle équilatéral est donné par les pentes des droites.
CongEjz9 a écrit: Je comprend bien qu'il faut minimiser une fonction linéaire contenant ces trois d mais quelles sont les coefficients ? Si, quelles sont les coefficients de la matrice colonne c ?
Je ne vais pas te le dire, ça serait faire l'exo à ta place. Réfléchis ! On cherche à "faire monter" la droite horizontale le plus haut possible, à "faire descendre" la droite qui supporte le côté droit le plus possible, etc.
CongEjz9 a écrit:Les contraintes sont-elles bien de la forme donné par l'indice ?
En gros, par exemple, si je donne n=5 points tels que, au hasard, (3,3) (3,4) (4,4) (5,5) et (2,5) sont les points donnés, comment se présenterai mon programme linéaire ?
Encore une fois, hors de question que je fasse l'exo à ta place. Réfléchis à partir des indices qui te sont fournis et de l'indication que j'ai donnée sur la nature des contraintes portant sur
CongEjz9 a écrit:PS: Il existe un problème du plus petit cercle contenant n points, cad un problème similaire à celui-ci mais ici on utilise un triangle équilatéral. La méthode utilisée d'après la littérature et Wikipédia est la programmation linéaire. Le fait que l'on utilise la programmation linéaire pour résoudre notre problème est donc justifiable, et puis ça fait aussi un bon exercice. Il n'est pas forcément nécessaire d'avoir un intérêt. Je suis d'accord que la programmation non-linéaire serait plus simple, il suffirait de minimiser l'aire du triangle équilatéral mais ici je galère... s'agirait-il de minimiser le périmètre ? Cad. A ce moment là, si on remplace les d par leur valeurs, il s'agirait de minimiser
et ça me semble louche.
Qui parle d'optimisation non linéaire ? Le problème se traite tout bêtement en prenant un maximum (ou des minima) de
Robot a écrit:Absolument pas ! Le fait que ce soit un triangle équilatéral est donné par les pentes des droites.
Je ne vais pas te le dire, ça serait faire l'exo à ta place. Réfléchis ! On cherche à "faire monter" la droite horizontale le plus haut possible, à "faire descendre" la droite qui supporte le côté droit le plus possible, etc.
Encore une fois, hors de question que je fasse l'exo à ta place. Réfléchis à partir des indices qui te sont fournis et de l'indication que j'ai donnée sur la nature des contraintes portant sur.
Qui parle d'optimisation non linéaire ? Le problème se traite tout bêtement en prenant un maximum (ou des minima) devaleurs.
Si j'ai bien compris, mes contraintes seraient de trouver les n (ou plus) inégalités en utilisant alpha. Si alpha positif alors les points sont dans le triangle. Donc on fixe alpha >= 0. Après il faudrait trouver les pentes des droites définissants le triangle (0 , sqrt3 et -sqrt3).
Euh ... d'après ce que tu écris, je ne suis pas sûr que tu aies bien compris. Me suis-je mal exprimé ? Je retente un coup.
Je note) , pour
, pour 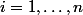 les points. (Entendons-nous bien, les
les points. (Entendons-nous bien, les  en haut ne sont pas des puissances, d'accord ?)
en haut ne sont pas des puissances, d'accord ?)
La droite du bas du triangle recherché a une équation de la forme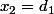 . (ça t'est donné dans les indices). Les
. (ça t'est donné dans les indices). Les  points sont "du bon côté" de cette droite (c.-à-d. ils sont tous au dessus) quand on a
points sont "du bon côté" de cette droite (c.-à-d. ils sont tous au dessus) quand on a  pour
pour 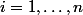 ; ça te donne des contraintes linéaires (portant uniquement sur
; ça te donne des contraintes linéaires (portant uniquement sur  ). Pour avoir le triangle le plus petit possible, on cherche a monter cette droite horizontale le plus haut possible, c.-à-d. à avoir
). Pour avoir le triangle le plus petit possible, on cherche a monter cette droite horizontale le plus haut possible, c.-à-d. à avoir  le plus grand possible (clair ? fais-toi un dessin dans ta tête). La "fonction d'objectif" à minimiser (fonction linéaire de
le plus grand possible (clair ? fais-toi un dessin dans ta tête). La "fonction d'objectif" à minimiser (fonction linéaire de  ) doit posséder la propriété de décroître quand
) doit posséder la propriété de décroître quand  croit ; ça te dit quelque chose sur le signe du coefficient de
croit ; ça te dit quelque chose sur le signe du coefficient de  dans la fonction d'objectif.
dans la fonction d'objectif.
Voila. Dans le paragraphe ci-dessus je ne me suis occupé que du côté bas du triangle, c.-à-d. je ne me suis occupé que de . Je te laisse t'occuper des deux autres côtés (c.-à-d. de
. Je te laisse t'occuper des deux autres côtés (c.-à-d. de  et
et 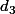 ). Les équations de ces deux autres côtés te sont données dans les indices, ton travail est tout mâché !
). Les équations de ces deux autres côtés te sont données dans les indices, ton travail est tout mâché !
Tu seras sans doute troublé par le fait que tu n'as pas assez d'information pour déterminer la fonction d'objectif, même à un facteur positif près. C'est normal, il y a une infinité de choix possibles et il suffit de choisir une fonction d'objectif qui a les propriétés voulues (autant la prendre la plus simple possible).
Le fait que les contraintes ne portent que sur une seule des variables à la fois explique pourquoi je dis qu'il est complètement farfelu de se poser ce problème comme un problème d'optimisation linéaire.
à la fois explique pourquoi je dis qu'il est complètement farfelu de se poser ce problème comme un problème d'optimisation linéaire.
Je note
La droite du bas du triangle recherché a une équation de la forme
Voila. Dans le paragraphe ci-dessus je ne me suis occupé que du côté bas du triangle, c.-à-d. je ne me suis occupé que de
Tu seras sans doute troublé par le fait que tu n'as pas assez d'information pour déterminer la fonction d'objectif, même à un facteur positif près. C'est normal, il y a une infinité de choix possibles et il suffit de choisir une fonction d'objectif qui a les propriétés voulues (autant la prendre la plus simple possible).
Le fait que les contraintes ne portent que sur une seule des variables
Robot a écrit:Euh ... d'après ce que tu écris, je ne suis pas sûr que tu aies bien compris. Me suis-je mal exprimé ? Je retente un coup.
Je note, pour
les points. (Entendons-nous bien, les
en haut ne sont pas des puissances, d'accord ?)
La droite du bas du triangle recherché a une équation de la forme. (ça t'est donné dans les indices). Les
points sont "du bon côté" de cette droite (c.-à-d. ils sont tous au dessus) quand on a
pour
; ça te donne des contraintes linéaires (portant uniquement sur
). Pour avoir le triangle le plus petit possible, on cherche a monter cette droite horizontale le plus haut possible, c.-à-d. à avoir
le plus grand possible (clair ? fais-toi un dessin dans ta tête). La "fonction d'objectif" à minimiser (fonction linéaire de
) doit posséder la propriété de décroître quand
croit ; ça te dit quelque chose sur le signe du coefficient de
dans la fonction d'objectif.
Voila. Dans le paragraphe ci-dessus je ne me suis occupé que du côté bas du triangle, c.-à-d. je ne me suis occupé que de. Je te laisse t'occuper des deux autres côtés (c.-à-d. de
et
). Les équations de ces deux autres côtés te sont données dans les indices, ton travail est tout mâché !
Tu seras sans doute troublé par le fait que tu n'as pas assez d'information pour déterminer la fonction d'objectif, même à un facteur positif près. C'est normal, il y a une infinité de choix possibles et il suffit de choisir une fonction d'objectif qui a les propriétés voulues (autant la prendre la plus simple possible).
Le fait que les contraintes ne portent que sur une seule des variablesà la fois explique pourquoi je dis qu'il est complètement farfelu de se poser ce problème comme un problème d'optimisation linéaire.
Merci beaucoup pour votre réponse, c'est vraiment plus clair. Du coup j'ai pu trouver les contraintes pour les autres d. J'ai commencé différemment hier mais je pense que c'est quand proche de votre méthode. Voilà ma nouvelle méthode:
Je choisi un triangle, je prend un point (x,y) et une distance d positive. Je choisi ensuite un triangle au hasard tel que sa base est parallèle à l'axe des x et dont le sommet est au dessus de sa base. On peut traduire les positions des trois sommets du triangle dans le repère par (
Ensuite, concernant le côté gauche, l'inégalité doit vérifier
Finalement, au côté droit,
Du coup je dois minimiser d tel que
où
Mon nouveau soucis, c'est lorsque je veux tester mon programme sur Matlab pour n=5 points (les mêmes que ceux en haut, i.e. (3,3) (3,4) (4,4) (4,5) (2,5)), je reçois une erreur qui me dit que le problème n'a pas assez de contraintes. J'utilise la commande linprog et je force l'utilisation du Simplexe (les autres c'est pareil). Mes matrices ressemblent à ça:
J'ai passé pas mal de temps à débugger le code, mais voilà là j'ai l'impression que ça ne veut juste pas fonctionner xD
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
