Bonjour à tous,
Je cherche à réaliser un petit programme qui puisse convertir un nombre hexadécimal en duodécimal.
Cela fait plusieurs heures que je me creuse la tête sans y parvenir... N'étant pas très doué en maths, je me tourne vers vous les experts !
Quelqu'un pourrait-il m'aider quand à l'algorithme à utiliser ?
Merci pour votre aide.
Conversion base 16 -> base 12
12 messages
- Page 1 sur 1
par Cyril Mar » 11 Juin 2008, 12:58
Bonjour !
J'espère qu'il n'est pas trop tard.
Soit m un nombre. Soit n le nombre de chiffres de m écrit en base 16. Multiplie le 1-er chiffre en partant de la gauche par 16 élevé à la puissance 0, le 2-ème chiffre par 16 élevé à la puissance 1, le 3-ème chiffre par 16 élevé à la puissance 2, ... , le (n - 1)-ème chiffre par 16 élevé à la puissance (n - 2) et le n-ème chiffre par 16 élevé à la puissance (n - 1).
Tu obtiens le nombre m écrit en base 10. Il ne te reste plus qu'à l'écrire sous la forme suivante : m = a1 * 12^(p - 1) + a2 * 12^(p - 2) + ... + a(p - 2) * 12^2 + a(p - 1) * 12^1 + ap * 12^0. D'où, écrit en base 12, m sera égal à a1a2 ... a(p - 2)a(p - 1)ap (a1, a2, etc., étant considérés comme des chiffres).
Par exemple, soit m = FD6 un nombre écrit en base 16.
En base 10, m = 15 * 16^2 + 13 * 16^1 + 6 * 16^0
En base 10, m = 15 * 256 + 13 * 16 + 6 * 1
En base 10, m = 3840 + 208 + 6
En base 10, m = 4054.
Or, 4054 = 337 * 12 + 10
Or, 4054 = (28 * 12 + 1) * 12 + 10
Or, 4054 = ((2 * 12 + 4) * 12 + 1) * 12 + 10
Or, 4054 = ((2 * 12 + 4) * 12 + 1) * 12^1 + 10 * 12^0
Or, 4054 = ((2 * 12 + 4) * 12^2 + 1 * 12^1 + 10 * 12^0
Or, 4054 = 2 * 12^3 + 4 * 12^2 + 1 * 12^1 + 10 * 12^0.
D'où, écrit en base 12, m = 241A.
Bon courage !
J'espère qu'il n'est pas trop tard.
Soit m un nombre. Soit n le nombre de chiffres de m écrit en base 16. Multiplie le 1-er chiffre en partant de la gauche par 16 élevé à la puissance 0, le 2-ème chiffre par 16 élevé à la puissance 1, le 3-ème chiffre par 16 élevé à la puissance 2, ... , le (n - 1)-ème chiffre par 16 élevé à la puissance (n - 2) et le n-ème chiffre par 16 élevé à la puissance (n - 1).
Tu obtiens le nombre m écrit en base 10. Il ne te reste plus qu'à l'écrire sous la forme suivante : m = a1 * 12^(p - 1) + a2 * 12^(p - 2) + ... + a(p - 2) * 12^2 + a(p - 1) * 12^1 + ap * 12^0. D'où, écrit en base 12, m sera égal à a1a2 ... a(p - 2)a(p - 1)ap (a1, a2, etc., étant considérés comme des chiffres).
Par exemple, soit m = FD6 un nombre écrit en base 16.
En base 10, m = 15 * 16^2 + 13 * 16^1 + 6 * 16^0
En base 10, m = 15 * 256 + 13 * 16 + 6 * 1
En base 10, m = 3840 + 208 + 6
En base 10, m = 4054.
Or, 4054 = 337 * 12 + 10
Or, 4054 = (28 * 12 + 1) * 12 + 10
Or, 4054 = ((2 * 12 + 4) * 12 + 1) * 12 + 10
Or, 4054 = ((2 * 12 + 4) * 12 + 1) * 12^1 + 10 * 12^0
Or, 4054 = ((2 * 12 + 4) * 12^2 + 1 * 12^1 + 10 * 12^0
Or, 4054 = 2 * 12^3 + 4 * 12^2 + 1 * 12^1 + 10 * 12^0.
D'où, écrit en base 12, m = 241A.
Bon courage !
par leon1789 » 11 Juin 2008, 19:01
Bonjour,
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base d'énumération...
Est-ce que cela vous parait moral ??? ...si ce n'est pas inutile ???
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base d'énumération...
Est-ce que cela vous parait moral ??? ...si ce n'est pas inutile ???
par leon1789 » 11 Juin 2008, 19:03
Bonjour,
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base de numération...
Est-ce que cela vous parait moral ??? (...si ce n'est pas inutile ???)
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base de numération...
Est-ce que cela vous parait moral ??? (...si ce n'est pas inutile ???)
par leon1789 » 11 Juin 2008, 19:03
Bonjour,
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base d'énumération...
Est-ce que cela vous parait moral ??? ...si ce n'est pas inutile ???
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base d'énumération...
Est-ce que cela vous parait moral ??? ...si ce n'est pas inutile ???
par leon1789 » 11 Juin 2008, 19:07
Bonjour,
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base de numération...
Est-ce que cela vous parait moral ??? (...si ce n'est pas inutile ???)
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base de numération...
Est-ce que cela vous parait moral ??? (...si ce n'est pas inutile ???)
par nuage » 11 Juin 2008, 22:00
Salut leon1789
C'est en effet immoral et inutile.
Mais la suggestion de Cyril Mar fonctionne, même si il est certain qu'on peut faire mieux.
Je te laisse le soin d'écrire l'algorithme direct.
Moi je suis paresseux.
leon1789 a écrit:Bonjour,
Ca me rappelle une discussion où une personne me soutenait qu'il fallait passer par la base 10 pour faire des changements de base de numération...
Est-ce que cela vous parait moral ??? (...si ce n'est pas inutile ???)
C'est en effet immoral et inutile.
Mais la suggestion de Cyril Mar fonctionne, même si il est certain qu'on peut faire mieux.
Je te laisse le soin d'écrire l'algorithme direct.
Moi je suis paresseux.
par leon1789 » 12 Juin 2008, 07:32
En fait, l'algo se situe dans la seconde partie des calculs de Cyril Mar : la première partie est de la "cuisine interne à son mode de calcul" si je peux dire.
De plus, si on faisait des conversions de flottants, le passage par une tiers base augmenterait les erreurs d'arrondi... Mais ici, on veut travailler sur des nombres entiers (donc pas d'erreur d'arrondi en vue).
Un algo de 3 ou 4 lignes est possible, mais une question "piège" se pose : comment le nombre 0 doit-il s'écrire ?
De plus, si on faisait des conversions de flottants, le passage par une tiers base augmenterait les erreurs d'arrondi... Mais ici, on veut travailler sur des nombres entiers (donc pas d'erreur d'arrondi en vue).
Un algo de 3 ou 4 lignes est possible, mais une question "piège" se pose : comment le nombre 0 doit-il s'écrire ?
grands nombres
par mathelot » 12 Juin 2008, 07:57
bjr,
on peut considérer une division euclidienne comme celle effectuée à l'école
française en classe de CM2, en divisant N par le chiffre 12=C , l'écriture de la division
s'effectuant en base 16.
On écrit le dividende en base 16,
N=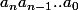
et l'on divise par le chiffre 12=C:
si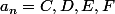
on obtient le premier chiffre du quotient Q ,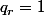
et le premier reste partiel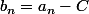
si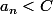
on calcule un dividende partiel:
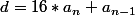en regroupant les deux premiers chiffres de N, et le premier chiffre (base 16) du quotient Q est obtenu en divisant d par C.
A la fin de la division, le reste final est inférieur à 12, c'est un chiffre base 16, et aussi le chiffre des unités de N ,en base 12. on recommence alors en prenant comme nouveau dividende le quotient Q obtenu:
pour obtenir le chiffre de poids 1 ("dizaine") de N en base 12.
Grosso modo, on calcule les chiffres de N base 12 par l'algorithme habituel de division de N par 12, les écritures se faisant en base 16.
Après, question implémentation:
a) ou l'on considère que la machine travaille naturellement en base 16
et on a juste à faire des divisions par 12, :zen:
b) ou alors on écrit les chiffres dans un tableau (par ex, du type unsigned int en C) et il faut tout programmer à la main. A toi de voir.
on peut considérer une division euclidienne comme celle effectuée à l'école
française en classe de CM2, en divisant N par le chiffre 12=C , l'écriture de la division
s'effectuant en base 16.
On écrit le dividende en base 16,
N=
et l'on divise par le chiffre 12=C:
si
on obtient le premier chiffre du quotient Q ,
et le premier reste partiel
si
on calcule un dividende partiel:
A la fin de la division, le reste final est inférieur à 12, c'est un chiffre base 16, et aussi le chiffre des unités de N ,en base 12. on recommence alors en prenant comme nouveau dividende le quotient Q obtenu:
pour obtenir le chiffre de poids 1 ("dizaine") de N en base 12.
Grosso modo, on calcule les chiffres de N base 12 par l'algorithme habituel de division de N par 12, les écritures se faisant en base 16.
Après, question implémentation:
a) ou l'on considère que la machine travaille naturellement en base 16
et on a juste à faire des divisions par 12, :zen:
b) ou alors on écrit les chiffres dans un tableau (par ex, du type unsigned int en C) et il faut tout programmer à la main. A toi de voir.
petits nombres ne dépassant pas les capacités de stockage
par mathelot » 12 Juin 2008, 08:39
re,
voilà un algo:
on note (q,r)=[a:b] quotient et reste de la division euclidienne de a par b.
N=nombre en entrée
i=0
tant que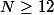
, faire:
(Q,r)=[N:12]
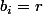chiffre de poids i.
i=i+1
N=Q
fintantque
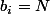(chiffre de poids fort)
renvoyer les chiffres de N en base 12:)
voilà un algo:
on note (q,r)=[a:b] quotient et reste de la division euclidienne de a par b.
N=nombre en entrée
i=0
tant que
(Q,r)=[N:12]
i=i+1
N=Q
fintantque
renvoyer les chiffres de N en base 12:
par Cyril Mar » 12 Juin 2008, 10:35
Effectivement, je croyais que mon action serait moralement bonne, étant donné que personne n'avait jusqu'ici trouvé utile de répondre à psychozx.
J'ai cru comprendre que psychozx n'avait pas un niveau très élevé en mathématiques (peut-être étudiant(e) en sciences humaines...). J'ai essayé de faire clair (tant pis pour la cuisine).
J'ai cru comprendre que psychozx n'avait pas un niveau très élevé en mathématiques (peut-être étudiant(e) en sciences humaines...). J'ai essayé de faire clair (tant pis pour la cuisine).
par leon1789 » 12 Juin 2008, 13:45
Cyril Mar a écrit:Effectivement, je croyais que mon action serait moralement bonne, étant donné que personne n'avait jusqu'ici trouvé utile de répondre à psychozx.
J'ai cru comprendre que psychozx n'avait pas un niveau très élevé en mathématiques (peut-être étudiant(e) en sciences humaines...). J'ai essayé de faire clair (tant pis pour la cuisine).
J'ai poussé un peu loin le bouchon, c'est vrai :marteau: , mais j'ai vu "rouge" quand j'ai vu base 10 --> base 12 >>...
mathelot a écrit:voilà un algo: (...)
oui, et on voit que peu importe la base dans laquelle N est donné : N est un nombre "abstrait", sans base. Un nombre n'a pas besoin de base pour "exister". La base est là pour faire une passerelle entre l'abstrait et la feuille de papier (ou la page web). L'algo fonctionne quelle que soit la manière dont on code les nombres pendant les calculs (en base 2, 10, ou sans base mais autrement, etc.).
Cela dit, l'algo renvoie
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :