bonjour
j'ai pas bien compris la différence entre suite de fonction converge uniformément et simplement
on a convergent simple cad on voit la convergent point par point c'est comme les suites
et la convergent uniforme a partir certain rang toutes les fn ne dépasse pas la limite
vous pouvez me donner géométriquement fonction converge simplement mais ne converge pas uniformément
merci d'avance
Convergence uniforme
6 messages
- Page 1 sur 1
Re: convergence uniforme
Salut,
LE exemple de base, c'est la suite de fonctions_{n\geq 1}) telle que
telle que  .
.
Si on fixe un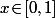 et qu'on regarde, pour ce
et qu'on regarde, pour ce  fixé la limite
fixé la limite =\lim_{n\to\infty}x^n) alors c'est tout simplement la limite d'une suite géométrique et on sait que la limite est
alors c'est tout simplement la limite d'une suite géométrique et on sait que la limite est  si
si  et il est clair que la limite est 1 si
et il est clair que la limite est 1 si 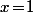 (la suite est constante égale à 1).
(la suite est constante égale à 1).
Cela signifie (par définition) que la suite de fonction_{n\geq 1}) converge simplement vers la fonction
converge simplement vers la fonction  égale à 0 sur
égale à 0 sur 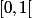 et égale à 1 en
et égale à 1 en 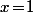 .
.
Y-a-t-il convergence uniforme ?
Par définition, il faut évaluer pour tout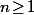 la "distance maximale" qu'il y a entre
la "distance maximale" qu'il y a entre  et
et  , c'est à dire
, c'est à dire 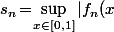\!-\!f(x)|) puis regarder si cette "distance maximale" tend ou pas vers 0 lorsque
puis regarder si cette "distance maximale" tend ou pas vers 0 lorsque 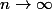 .
.
Ici,\!-\!f(x)|=x^n) si
si  et
et \!-\!f(1)|=0) donc l'image de [0,1] par la fonction
donc l'image de [0,1] par la fonction  est [0,1[ qui a comme borne supérieure 1 (borne non atteinte)
est [0,1[ qui a comme borne supérieure 1 (borne non atteinte)
Donc la "distance maximale" est pour tout
pour tout 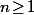 qui ne tend évidement pas vers 0 lorsque
qui ne tend évidement pas vers 0 lorsque 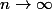 ce qui signifie que la suite de fonctions
ce qui signifie que la suite de fonctions _{n\geq 1}) ne converge pas uniformément vers la fonction
ne converge pas uniformément vers la fonction  .
.
LE exemple de base, c'est la suite de fonctions
Si on fixe un
Cela signifie (par définition) que la suite de fonction
Y-a-t-il convergence uniforme ?
Par définition, il faut évaluer pour tout
Ici,
Donc la "distance maximale" est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: convergence uniforme
Bonjour !
Tu comprendras mieux à l'aide d'un dessin : supposons que soit limite simple de la suite
soit limite simple de la suite 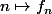 .
.
Fais un schéma où tu représentes les courbes,\;y=f(x)-\varepsilon,\;y=f(x)+\varepsilon,\;y=f_n(x)) .
.
Quand il y a convergence uniforme, pour assez grand, la courbe d'équation
assez grand, la courbe d'équation ) est toute entière dans la "bande" de frontières représentant
est toute entière dans la "bande" de frontières représentant  .
.
Fais ce dessin pour l'exemple=x^n) .
.
Tu comprendras mieux à l'aide d'un dessin : supposons que
Fais un schéma où tu représentes les courbes
Quand il y a convergence uniforme, pour
Fais ce dessin pour l'exemple
Re: convergence uniforme
Bonjour,
Ci-joint un aperçu : http://www.bibmath.net/dico/index.php?a ... c/cvu.html
Voir aussi tout en bas de la page : la convergence uniforme a mis du temps avant d'être perçue !
Ci-joint un aperçu : http://www.bibmath.net/dico/index.php?a ... c/cvu.html
Voir aussi tout en bas de la page : la convergence uniforme a mis du temps avant d'être perçue !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
