Convergence uniforme et integrale

par **praud** » 06 Nov 2007, 00:01

Soit n>1 et\

.
fn converge simplement sur[0,1] vers

Mais comment montrer qu'elle converge uniformément vers[a,1] pour tout

c'est a dire montrer que la limite

or

comment calcule t-on la valeur de l'integrale suivante

MERCI

par **yos** » 06 Nov 2007, 08:27

praud a écrit:comment montrer qu'elle converge uniformément vers[a,1] pour tout c'est a dire montrer que la limite or

C'est majoré par

qui tend vers 0.

praud a écrit:comment calcule t-on la valeur de l'integrale suivante

Tu veux l'intégrale ou bien sa limite qd n tend vers l'infini?

par **praud** » 06 Nov 2007, 09:11

yos a écrit:C'est majoré par qui tend vers 0.

Tu veux l'intégrale ou bien sa limite qd n tend vers l'infini?

Tu as montre que

tend vers 0 mais il ne faut-il pas montrer que le sup de

?
OUI je recherche la limite quand n tend vers l'infini.

par **yos** » 06 Nov 2007, 09:50

J'ai majoré par un truc qui ne dépend pas de x, donc ma majoration est uniforme (elle majore le sup en x de

).

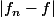
Pour l'autre question, tu peux dire que

tend vers

(à cause de la cvu).
Cette dernière intégrale se calcule par des intégrations par parties successives puisque

.
Ensuite on fait tendre a vers 0.