Convergence de n!/n^n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
RaoulBoch
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2007, 15:08
-
 par RaoulBoch » 05 Nov 2007, 13:57
par RaoulBoch » 05 Nov 2007, 13:57
Soit (Un) la suite definie par
;)n;);) Un = (n!) / (n^n)
Etudier la convergence de (Un)
Merci de me débloquer
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Nov 2007, 14:03
par Nightmare » 05 Nov 2007, 14:03
Bonjour :happy3:
Remarque que

:happy3:
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:15
par thedream01 » 05 Nov 2007, 14:15
Bonjour!
Sauf erreur de ma part, je dirais plutot:
U(n+1) = U(n) * (n/(n+1))^n.
tu vois comment conclure?
-
RaoulBoch
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2007, 15:08
-
 par RaoulBoch » 05 Nov 2007, 14:16
par RaoulBoch » 05 Nov 2007, 14:16
attendez je regarde l'autre methode
-
RaoulBoch
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2007, 15:08
-
 par RaoulBoch » 05 Nov 2007, 14:21
par RaoulBoch » 05 Nov 2007, 14:21
ca serait pas plutot
Un+1= Un * (n+1) * (n/n+1)^n ???
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:36
par thedream01 » 05 Nov 2007, 14:36
revérifie tes calculs
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Nov 2007, 14:38
par ThSQ » 05 Nov 2007, 14:38
Ca tend vers zéro est très très vite !
1- Par récurration c'est facile de montrer que

2- Ou
^n)
par l'utilisation de Moyenne arithmétique >= moyenne géométrique et donc

3- Ou Stirling
... :briques:
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:41
par thedream01 » 05 Nov 2007, 14:41
Il n'est pas la peine de se compliquer la vie comme ça!!!
Il suffit de remarque que n/(n+1) < 1. Donc que U(n+1) < U(n) pour n>0.
Ta suite est minorée par 0 d'où la convergence!
-
RaoulBoch
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2007, 15:08
-
 par RaoulBoch » 05 Nov 2007, 14:41
par RaoulBoch » 05 Nov 2007, 14:41
tu peux developper un peu stp
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:42
par thedream01 » 05 Nov 2007, 14:42
Comment utiliser Stirling???
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 05 Nov 2007, 14:43
par bitonio » 05 Nov 2007, 14:43
n!~

et sinon il suffit de dire que
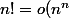)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Nov 2007, 14:44
par ThSQ » 05 Nov 2007, 14:44
thedream01 a écrit:Il n'est pas la peine de se compliquer la vie comme ça!!!
Il suffit de remarque que n/(n+1) 0.
Ta suite est minorée par 0 d'où la convergence!
Certes elle converge. Et vers quoi ?
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:45
par thedream01 » 05 Nov 2007, 14:45
Il ne faut pas te compliquer la vie, tu as une suite décroissante et minorée, donc elle converge!
Qu'est-ce que tu n'as pas compris?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Nov 2007, 14:46
par ThSQ » 05 Nov 2007, 14:46
J'ai pas compris pourquoi elle converge vers zéro (avec juste les faits que décroissant + > 0). Mais si tu me l'expliques lentement je vais peut-être comprendre !
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 05 Nov 2007, 14:47
par bitonio » 05 Nov 2007, 14:47
Rien ne prouve que si elle est décroissante et minorée elle tend vers 0...
-
thedream01
- Membre Relatif
- Messages: 289
- Enregistré le: 20 Avr 2007, 10:57
-
 par thedream01 » 05 Nov 2007, 14:48
par thedream01 » 05 Nov 2007, 14:48
On ne nous a pas demandé la limite!
On nous a demandé si elle convergait ou non!
Aprés, il est évident qu'elle tend vers zéro, chose que l'on peut démontrer comme vous l'avez fait avc Stirling...(mais je ne pense pas qu'on connaisse ça en début de Sup, du moins, on ne l'avait pas vu nous)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Nov 2007, 14:51
par ThSQ » 05 Nov 2007, 14:51
En général quand on demande d'étudier la convergence on demande aussi la valeur de la limite. Bref. J'arrête ici cette discussion inutile.
-
RaoulBoch
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Sep 2007, 15:08
-
 par RaoulBoch » 05 Nov 2007, 14:53
par RaoulBoch » 05 Nov 2007, 14:53
On a Un+1 = Un * (n+1) * (n/n+1)^n *1/(n+1)
donc comme (n/n+1)^n tend vers 0 quand n tend vers plus l'infini on a quand n tend vers plus l'infini Un+1 = 0
et donc avec le théoreme de passage a la limite, l =0
on peut faire ca?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Nov 2007, 15:00
par ThSQ » 05 Nov 2007, 15:00
RaoulBoch a écrit:(n/n+1)^n tend vers 0 quand n tend vers plus l'infini
Sûr ? :hein:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Nov 2007, 15:01
par yos » 05 Nov 2007, 15:01
Bonjour.
^n)
tend vers 1/e et pas vers 0. Cela permet de conclure car on a
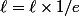
donc
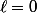
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
