Convergence de suites (encore...)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 12 Sep 2009, 18:45
par Edward » 12 Sep 2009, 18:45
Bonsoir,
Je bloque sur un exercice :
Soit
)
définie par

,

et
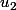
strictements positifs et
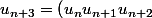^{\frac{1}{3}})
. Montrer que
)
converge et trouver sa limite. On pourra noter
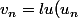)
et vérifier que

est constant.
J'ai réussi à prouver l'indication mais je n'arrive pas à montrer que u converge. En fait je n'arrive pas trop à voir comment l'indication peut aider...
Quelqu'un aurait-il une idée ?
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 12 Sep 2009, 19:31
par euler21 » 12 Sep 2009, 19:31
Bonsoir:
Si tu appelles C cette constante et que tu considères la suite définie par w(n)=v(n)- (1/6)*C. Alors w(n) est une suite récurrente du deuxième ordre.
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 12 Sep 2009, 19:42
par Edward » 12 Sep 2009, 19:42
Je viens de comprendre. Voila une méthode à retenir ^^. Je pense que ça devrait aller maintenant. Merci beaucoup Euler :++:
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 12 Sep 2009, 19:50
par euler21 » 12 Sep 2009, 19:50
Je t'en prie :++:
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 12 Sep 2009, 20:19
par Edward » 12 Sep 2009, 20:19
Après calculs je tombe vraiment sur un truc TRES moche. Mon discriminant pour la suite récurrente d'ordre 2 est négatifs et la solution ne se simplifie pas sous forme simple. Est-ce que j'ai fait une erreur quelque part ?
EDIT : je trouve comme solution de l'équation caractéristique

et son conjugué
-
Edward
- Membre Relatif
- Messages: 150
- Enregistré le: 13 Jan 2008, 11:58
-
 par Edward » 12 Sep 2009, 20:54
par Edward » 12 Sep 2009, 20:54
Finalement c'est bon, il se trouve qu'avec le discriminant négatif, j'obtient une solution bornée donc qui part quand n tend vers l'infini. Ouf...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités