Convergence de la méthode du gradient a pas fixe

[lila bouzar]

bonjour, je dois démontrer que si X(k+1)=X(k)+ c ( B - A X(k) ) avec A X=B le système linéaire à résoudre, et si A est diagonale strictement dominante et vérifie a(ii)>0 et si 0< c < 1/ max(a(ii)) alors cette méthode est convergente.
C'est la méthode du gradient à pas fixe, ici c est constant
si vous avez une idée ou une piste répondez moi svp merci beaucoup

[girdav]

Bonjour,
on doit montrer que la matrice a un rayon spectral strictement inférieur à . Pour cela, on peut prendre une valeur propre et un vecteur propre x associé. On peut écrire l'égalité pour la coordonnée qui réalise le max des 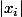. On regroupe d'un côté tout ce qui a à voir avec . Ensuite on passe aux valeurs absolues, dans l'idée d'utiliser le fait que la matrice soit à diagonale strictement dominante.