Bonjour tout le monde.
Voila je suis un peu désespéré je ne comprends rien.
Je ne comprends pas qu'est ce que la convergence uniforme.
Rn(x) tends vers 0? c'est ça ?
Quelles sont les méthodes ?
Je ne comprends rien non plus a la convergence normal.
Quelles sont les méthodes ?
Converge et serie de fonctions
4 messages
- Page 1 sur 1
La convergence uniforme, c'est une méthode générale pour assurer la continuité d'une limite de fonctions :
-si_{n\in\mathbb{N}}) est une suite de fonctions définies de I (où I est un segment) dans un e.v.n.
est une suite de fonctions définies de I (où I est un segment) dans un e.v.n. ) , si f est une fonction définie sur I telle que
, si f est une fonction définie sur I telle que 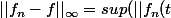-f(t)||_F), t\in I) existe et tend vers 0 quand n tend vers l'infini, on dit que la suite
existe et tend vers 0 quand n tend vers l'infini, on dit que la suite ) converge uniformément vers f.
converge uniformément vers f.
On a la propriété que : si les sont toutes continues sur I, f a le bon goût de l'être aussi.
sont toutes continues sur I, f a le bon goût de l'être aussi.
Apparemment, vu ton message, tu parles de séries de fonctions. Ca ne change rien. La notion est la même, sauf que la série que tu considères est simplement la suite=(\sum_{k=0}^{n}{g_k})) (série de terme général
(série de terme général 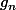 ).
).
La convergence normale, c'est une condition suffisante pour assurer la convergence uniforme d'une série de fonctions :
-si on a une série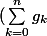) de fonctions définies sur un intervalle I, si
de fonctions définies sur un intervalle I, si  est le terme général d'une série convergente (dans
est le terme général d'une série convergente (dans  , puisqu'il s'agit d'une norme !), alors on dit que la série de fonctions converge normalement sur I.
, puisqu'il s'agit d'une norme !), alors on dit que la série de fonctions converge normalement sur I.
En particulier, cela implique qu'elle converge uniformément sur I (vers sa limite, qui ne peut être que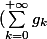) .
.
Pour autant, ce n'est pas une condition nécessaire de convergence uniforme (on peut très bien avoir : converge sans que
converge sans que  ne converge !).
ne converge !).
Cela clarifie-t-il tes idées ? Sinon, quels sont tes problèmes ?
(Deux conseils, pour finir :
1-précise tes notations. Rn(x) ne veut rien dire pour quelqu'un qui n'a pas ton cours sous les yeux, les notations changent d'un prof à un autre, d'un humain à un autre...
2-précise où se situent les objets dont tu parles. Rn(x) tend vers 0, oui, soit, mais quand quoi tend vers quoi ? Quand n tend vers l'infini ? Quand x tend vers 0 ? Quand x tend vers 42 ?)
Bon courage !
-si
On a la propriété que : si les
Apparemment, vu ton message, tu parles de séries de fonctions. Ca ne change rien. La notion est la même, sauf que la série que tu considères est simplement la suite
La convergence normale, c'est une condition suffisante pour assurer la convergence uniforme d'une série de fonctions :
-si on a une série
En particulier, cela implique qu'elle converge uniformément sur I (vers sa limite, qui ne peut être que
Pour autant, ce n'est pas une condition nécessaire de convergence uniforme (on peut très bien avoir :
Cela clarifie-t-il tes idées ? Sinon, quels sont tes problèmes ?
(Deux conseils, pour finir :
1-précise tes notations. Rn(x) ne veut rien dire pour quelqu'un qui n'a pas ton cours sous les yeux, les notations changent d'un prof à un autre, d'un humain à un autre...
2-précise où se situent les objets dont tu parles. Rn(x) tend vers 0, oui, soit, mais quand quoi tend vers quoi ? Quand n tend vers l'infini ? Quand x tend vers 0 ? Quand x tend vers 42 ?)
Bon courage !
muse a écrit:Mais j'ai lu quelque part que
La série fn(x) converge normalement ssi:
supconvergeait vers 0 il avait Convergence normale. C'est vrai ça ou c'est uniforme? un coup je lis normalement et un coup uniformemennt
bonsoir
problème d'indice dans ta somme je présume qu'il faut lire k = n+1
des f k (x)
et dans ce cas c'est la convergence uniforme
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
