Converge de série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 31 Déc 2011, 18:50
par zork » 31 Déc 2011, 18:50
bonsoir,
soit (an) [n de 1 à oo] une suite de nombres réels. Soient 0=no=0 on pose

démontrer à partir de la définition de la convergence d'une série que si

converge alors la série

converge
comme la série an converge
an tend vers 0
|an|<epsilon
je prend epsilon=1 mais après je n'arrive pas
PS: quel est d'après vous le niveau de cet exo, facile, moyen, difficile? parce qu'en fac en TD je n'ai jamais fais de chose comme cela
je vous remercie pour votre aide
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 31 Déc 2011, 18:59
par girdav » 31 Déc 2011, 18:59
Bonjour,
on peut vérifier que la suite des sommes partielles est de Cauchy.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 31 Déc 2011, 19:06
par Matt_01 » 31 Déc 2011, 19:06
Perso, j'essaierai d'écrire les sommes partielles :
la somme des n premiers b_k :


.
.
.

Ne reconnais tu pas quasiment une somme partielle des a_k ?
(L'avantage ici c'est qu'on connait alors la somme des b_k)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 12:52
par zork » 01 Jan 2012, 12:52
je n'ai pas compris ce que tu as voulus dire MATT
sinon pour revenir à la méthode de Girdav
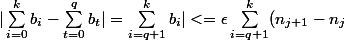<=n_{k+1} \epsilon)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 13:44
par girdav » 01 Jan 2012, 13:44
Attention, là tu ne te sers que du fait que

, mais on a plus fort que ça (en fait là c'est comme si tu devais enfoncer un clou avec un marteau, mais tu ne gardes que le manche et tu n'y arrives pas).
On pose

.
Prend un

, et un
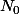
tel que si

alors

. Prend
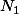
un entier tel que pour

,

. Vois-tu comment majorer

pour

?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 15:16
par zork » 01 Jan 2012, 15:16
mais là on connait la valeur de la somme qui est

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 16:44
par girdav » 01 Jan 2012, 16:44
Oui, et maintenant réécris cette somme en terme de
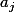
.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 16:46
par zork » 01 Jan 2012, 16:46
Pourquoi on prend un n1? ce n'est pas le critère de cauchy?
girdav a écrit:Prend un

, et un

tel que si

alors

. Prend
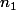
un entier tel que pour

,

. Vois-tu comment majorer

pour

?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 16:50
par girdav » 01 Jan 2012, 16:50
Ah, mauvais choix de notation, j'aurais du prendre des

.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 18:42
par zork » 01 Jan 2012, 18:42
pour moi le critère que tu as écris pour bk n'est pas cauchy. Peu importe N ou non
dans mon cours j'ai:
une série converge ssi pour tout

>0, il existe N tel que k,m>N avec k>m,

-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 19:26
par zork » 01 Jan 2012, 19:26
c'est bon j'ai réussit
par contre je n'arrive pas à montrer que

j'ai essayé de faire un changement d'indice dans bk pour partir de 1 mais j'y arrive pas
Finalement j'ai essayé de faire la différence mais ca ne marche pas non plus
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 20:26
par girdav » 01 Jan 2012, 20:26

puis on fait tendre

vers l'infini, maintenant que l'on sait que ces deux limites existent.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 01 Jan 2012, 23:12
par zork » 01 Jan 2012, 23:12
quel argument utilises-tu pour te ramener à une seule somme?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 01 Jan 2012, 23:49
par girdav » 01 Jan 2012, 23:49
Les ensembles

pour

forment une partition de

.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 02 Jan 2012, 16:12
par zork » 02 Jan 2012, 16:12
on ne peut pas faire autrement puisqu'en fac je n'ai jamais vu les partitions
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
