Continuité de l'application trace

[zaidoun]

Bonsoir,
Pourquoi l'application est continue?
avec X est une matrice de et com(A) est la commatrice de A.

[BiancoAngelo]

Bonsoir,

J'imagine que si je devais esquisser quelque chose, je dirais que la comatrice vient d'un calcul de déterminant, qui est continu.

Puis que la transposée change rien à la continuité, autant que pour le produit par X (vues les définitions des deux opérations).

Puis la trace X -> Tr (X) continue, non ?

Donc au final, on utilise que des fonctions continues...
Je ne sais pas si c'est valable, mais bon :)

[BiancoAngelo]

Néanmoins j'aurais écrit l'application :

, ça me paraît mieux comme ça, même si c'est pareil :ptdr:

[barbu23]

Bonsoir,

L'application proposée par zaidoun me fait penser à la différentielle de l'application déterminant qui est linéaire en dimension finie, donc nécessairement continue. Je ne sais pas si c'est le bon argument pour palier ce problème.

Cordialement. :happy3:

Edit : L'application déterminant est de classe ( Par construction ) en tout point , donc, sa différentielle est aussi de classe en tout point .

[Maxmau]

Bj
Cette application n'est-elle pas polynomiale ?

[zaidoun]

@barbu23: Oui exactement la différentielle de l'application déterminant.
Mais je pense pas que cette application est linéaire.

[barbu23]

@barbu23: Oui exactement la différentielle de l'application déterminant.
Mais je pense pas que cette application est linéaire.

Elle n'est pas linéaire en , mais linéaire en .
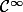
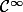
Elle est par contre continue en tout point , car l'application déterminant est une fonction polynomiales, donc, de classe en tout point , par conséquent, sa différentielle est aussi de classe en tout point , et donc, elle est continue en tout point .

[zaidoun]

Merci bien.
Juste une autre question concernant la différentiabilité d'un produit de deux applications différentiables.

Si f, g : U---> F sont différentiables, est ce que fg est différentiable?

avec U est un ouvert d'un espace vectoriel normé E et F est un espace vectoriel normé.

[Ben314]

Merci bien.
Juste une autre question concernant la différentiabilité d'un produit de deux applications différentiables.

Si f, g : U---> F sont différentiables, est ce que fg est différentiable?

avec U est un ouvert d'un espace vectoriel normé E et F est un espace vectoriel normé.

Tu le définit comment le produit de f et de g sachant qu'elles prennent leurs valeurs dans un e.v.n. ?

[zaidoun]

Donc on ne peut pas parler du produit dans un cas général.Il faut prendre F= R, c'est ça?

Car J'ai trouvé ça dans un cours avec F quelconque.J'étais surpris moi même par ce résultat.

[zaidoun]

@Ben314: c'est juste le raisonnement précédent? ou il existe d'autres cas pour le choix de F?

[SLA]

@Ben314: c'est juste le raisonnement précédent? ou il existe d'autres cas pour le choix de F?

En fait si tu muni F d'une forme bilinéaire continue (donc une sorte de produit) ça devient vrai pour F quelconque.

[Ben314]

Ben, pour pouvoir parler d'un "plus ou moins produit" de f par g, il y a des tas de cas où ça peut avoir du sens :
- Si f et g atterrissent dans un e.v. muni d'un produit scalaire tu peut faire le produit scalaire de f par g (qui donne un réel)
- Si f et g atterrissent dans R^3, tu peut faire le produit vectoriel de f par g (qui est un vecteur)
- Si f atterrit dans R et g atterrit dans un e.v.n., tu peut faire le produit "extérieur" de f par g (i.e. le produit d'un scalaire par un vecteur)
- En fait, tout ces cas de figurent peuvent se résumer à un seul "général" où tu as f:U->F, g:U->G où F et G sont des e.v.n. et où tu as aussi une forme bilinéaire continue B:FxG->H où H est aussi un e.v.n.
Tu peut alors considérer l'application U->H ; x -> B(f(x),g(x))

Dans tout les cas (donc dans le cas général...) tu as une formule pour la diférentielle du produit qui ressemble trés fortement à celle du cas des fonctions de R dans R.


Edit : Grilled par SLA... :ptdr: