Bonjour,
Suite à une méthode de prédiction de la valeur d'une variable aléatoire (la méthode quelle soit de régression ou autres importe peu à mon avis pour répondre à ma question) j'obtiens évidemment des résidus (différence entre la valeur réelle et ma prédiction) et je souhaiterais savoir comment faire pour construire un IC pour ma prédiction.
Mon idée est d'observer les résidus et de faire un test de normalité.
==> Si ils suivent une loi Normale alors on en calcule la variance empirque et on sait que pour la loi Normale plus de 95% des données sont comprises entre
[moyenne+2*sigma ; moyenne - 2*sigma]
avec sigma est l'écart type.
Donc on peut construire un IC à partir de l'écart type empirique observé sur les résidus.
Utilisable ou non ?? :hein:
PS : Je n'arrive pas à taper correctement les formules quelqu'un peut m'expliquer ?
Construction empirique d'un intervalle de confiance (IC)
8 messages
- Page 1 sur 1
Salut,
ton idée me semble bonne. Tu construis un intervalle de confiance pour les résidus (qui sont, en principe, aléatoires). Vérifie quand même que la moyenne des résidus et raisonnablement proche de zéro.
Une remarque pratique :
pour calculer la variance empirique il ne faut prendre pas la moyenne empirique mais la moyenne théorique égale à 0. Et il n'y a pas lieu de multiplier par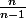
le test de Student est peut-être plus approprié, à moins que tu n'aies beaucoup de valeurs (enfin je crois, il faut que je réfléchisse, et là je dois nourrir ma petite famille)
En fait il n'est même pas indispensable que les résidus suivent une loi normale, il suffit qu'ils suivent une loi pour la quelle on sait construire un intervalle de confiance.
ton idée me semble bonne. Tu construis un intervalle de confiance pour les résidus (qui sont, en principe, aléatoires). Vérifie quand même que la moyenne des résidus et raisonnablement proche de zéro.
Une remarque pratique :
pour calculer la variance empirique il ne faut prendre pas la moyenne empirique mais la moyenne théorique égale à 0. Et il n'y a pas lieu de multiplier par
le test de Student est peut-être plus approprié, à moins que tu n'aies beaucoup de valeurs (enfin je crois, il faut que je réfléchisse, et là je dois nourrir ma petite famille)
En fait il n'est même pas indispensable que les résidus suivent une loi normale, il suffit qu'ils suivent une loi pour la quelle on sait construire un intervalle de confiance.
Salut,
mes excuses, quand j'ai écris ce message je pensais au cas où les résidus ont une répartition normale. Dans ce cas l'utilisation d'une loi (et non d'un test comme je l'ai malheureusement écrit) de Student me semble justifié.
Pour l'étude de la normalité des résultats, en effet un test de Kolmogorov ou un chi2, semblent utiles.
mes excuses, quand j'ai écris ce message je pensais au cas où les résidus ont une répartition normale. Dans ce cas l'utilisation d'une loi (et non d'un test comme je l'ai malheureusement écrit) de Student me semble justifié.
Pour l'étude de la normalité des résultats, en effet un test de Kolmogorov ou un chi2, semblent utiles.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
