Bonjour,
J'ai un exercice d'analyse/ algèbre sur le calcul du conditionnement_infini d'une matrice et je ne comprends pas comment faire,
la matrice est A =
( -5 1 0 i ;
-i 7 2 1 ;
1 1 10 0 ;
0 -1 0 4 )
il faut calculer II A II_infini et II A^-1II_infini puis multiplier les deux normes pour obtenir le conditionnement
Pourriez vous m'aider dans mes calculs ? ou bien en me donnant un exemple corrigé avec une autre matrice à coefficient complexe ?
Merci
Conditionnement d'une matrice
8 messages
- Page 1 sur 1
Re: Conditionnement d'une matrice
Salut,
Rappelons que si) est un vecteur de
est un vecteur de , alors par définition
, alors par définition)
Ensuite, si A est une matrice de) , la norme infinie de A est définie par :
, la norme infinie de A est définie par :

Mais tu as du voir (où alors, redémontre le) que dans le cas particulier de la norme infinie, on a :

Autrement dit, pour chacune des 4 lignes de ta matrices, tu fais la somme des coefficient en module et le maximum des 4 nombres obtenus est ta norme infinie.
Rappelons que si
Ensuite, si A est une matrice de
Mais tu as du voir (où alors, redémontre le) que dans le cas particulier de la norme infinie, on a :
Autrement dit, pour chacune des 4 lignes de ta matrices, tu fais la somme des coefficient en module et le maximum des 4 nombres obtenus est ta norme infinie.
Modifié en dernier par Elias le 30 Juin 2018, 10:08, modifié 1 fois.
Pseudo modifié : anciennement Trident2.
Re: Conditionnement d'une matrice
Bonjour,
donc pour la norme infini de A , je trouves
I -5 I + I 1 I + I 0 I + I i I = 5 + 1 +1 = 7
I -i I + I 7 I + I 2 I + I 1 I = 1 + 7 + 2 + 1 =11
I 1I + I 1 I + I 10 I = 12
I 0 I + I -1 I + I 0 I + I 4 I = 5
Donc le max est 12 donc norme de A = 12
Est-ça ?
donc pour la norme infini de A , je trouves
I -5 I + I 1 I + I 0 I + I i I = 5 + 1 +1 = 7
I -i I + I 7 I + I 2 I + I 1 I = 1 + 7 + 2 + 1 =11
I 1I + I 1 I + I 10 I = 12
I 0 I + I -1 I + I 0 I + I 4 I = 5
Donc le max est 12 donc norme de A = 12
Est-ça ?
Re: Conditionnement d'une matrice
Voilà !
Mais il faudra quand même que tu cherches à démontrer qu'avec le cas particulier de la norme infinie, ça revient à procéder comme cela (à partir de la définition de norme matricielle subordonnée à la norme infinie)
Mais il faudra quand même que tu cherches à démontrer qu'avec le cas particulier de la norme infinie, ça revient à procéder comme cela (à partir de la définition de norme matricielle subordonnée à la norme infinie)
Pseudo modifié : anciennement Trident2.
Re: Conditionnement d'une matrice
la réponse me parait très longue et un peu complexe, je me demande si c'est ce que mon enseignant attendait,
dans l'exercice complet, on a d'abord montré dans une question a) la relation suivante pour une matrice A de dimension (n,n) à diagonale strictement dominante
pour tout delta > 0 , I a_ii I >= somme pour j = 1, j différent de i allant jusque n des I a_ij I + delta
puis dans une question b) on a montré que II A -1 II_inf <= 1 / delta
La question c sur laquelle je bloque était : " Expliciter delta" et "montrer que cond(B) <= 4"
Voyez vous une autre méthode attendu par l'enseignant ?
Qu'entends t on par expliciter delta ? Faut il juste dire que plus delta est petit, plus conditionnement sera grand ?
dans l'exercice complet, on a d'abord montré dans une question a) la relation suivante pour une matrice A de dimension (n,n) à diagonale strictement dominante
pour tout delta > 0 , I a_ii I >= somme pour j = 1, j différent de i allant jusque n des I a_ij I + delta
puis dans une question b) on a montré que II A -1 II_inf <= 1 / delta
La question c sur laquelle je bloque était : " Expliciter delta" et "montrer que cond(B) <= 4"
Voyez vous une autre méthode attendu par l'enseignant ?
Qu'entends t on par expliciter delta ? Faut il juste dire que plus delta est petit, plus conditionnement sera grand ?
Re: Conditionnement d'une matrice
Oulaaaa, attention.
Pour moi, si) (où
(où  ou
ou  ), on dit que
), on dit que  est à diagonale strictement dominante si pour tout
est à diagonale strictement dominante si pour tout 
Ensuite, d'après ta question a), tu affirmerais que :
+ \delta)
On voit clairement que c'est pas possible : si tu prend , on voit que ça marche pas.
, on voit que ça marche pas.
Je pense que c'est plutôt ceci que dit la question a) :
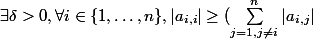+ \delta) (**)
(**)
____________________________________________________________________________
Après, tu as montré que , OK.
, OK.
Ensuite, la question "expliciter delta", c'est plutôt "donner UN exemple de delta qui marche parmi tous les delta existant vérifiant (**) (et ce qui est pas bête, c'est de donner le plus grand possible pour que 1/delta soit le plus petit possible).
Reprend ta matrice A (qui est à diagonale strictement dominante) et essaie de voir que convient.
convient.
Enfin, pour calculer le conditionnement de A (et non de B comme tu le marques), tu gardes ce que tu as fait pour le calcul de (tu as trouvé 12).
(tu as trouvé 12).
Et en fait, les questions d'avant te permettent d'éviter de te taper le calcul de (qui est théoriquement nécessaire pour calculer le conditionnement de A mais là, on te demande juste une majoration).
(qui est théoriquement nécessaire pour calculer le conditionnement de A mais là, on te demande juste une majoration).
Comme tu sais que et qu'on peut prendre
et qu'on peut prendre  , tu en déduis que :
, tu en déduis que :

Il vient alors :
 = ||A||_{\infty} \times ||A^{-1}||_{\infty} = 12 \times ||A^{-1}||_{\infty} \leq 12 \times 1/3=4.)
Pour moi, si
Ensuite, d'après ta question a), tu affirmerais que :
On voit clairement que c'est pas possible : si tu prend
Je pense que c'est plutôt ceci que dit la question a) :
____________________________________________________________________________
Après, tu as montré que
Ensuite, la question "expliciter delta", c'est plutôt "donner UN exemple de delta qui marche parmi tous les delta existant vérifiant (**) (et ce qui est pas bête, c'est de donner le plus grand possible pour que 1/delta soit le plus petit possible).
Reprend ta matrice A (qui est à diagonale strictement dominante) et essaie de voir que
Enfin, pour calculer le conditionnement de A (et non de B comme tu le marques), tu gardes ce que tu as fait pour le calcul de
Et en fait, les questions d'avant te permettent d'éviter de te taper le calcul de
Comme tu sais que
Il vient alors :
Pseudo modifié : anciennement Trident2.
Re: Conditionnement d'une matrice
Oui tu as raison , mes excuses j'ai mal recopier la formule sur le forum.. c'est bien (**)
J'avoue ne pas comprendre comment on obtient le delta égal à 3 ?
J'ai essayé de trouver les deltas pour lesquels nous aurions l'égalité (**) à savoir:
5 = 2 + 3
7 = 4 + 3
10 = 2 + 8
4 = 1 + 3
Le delta devant être le même pour toute les équations, ça ne pourrait pas être 8 et donc ce serait 3 ?
Je doutes de mon cheminement d'idée, mais je ne vois pas comment faire autrement ..
Merci
J'avoue ne pas comprendre comment on obtient le delta égal à 3 ?
J'ai essayé de trouver les deltas pour lesquels nous aurions l'égalité (**) à savoir:
5 = 2 + 3
7 = 4 + 3
10 = 2 + 8
4 = 1 + 3
Le delta devant être le même pour toute les équations, ça ne pourrait pas être 8 et donc ce serait 3 ?
Je doutes de mon cheminement d'idée, mais je ne vois pas comment faire autrement ..
Merci
Re: Conditionnement d'une matrice
C'est des "  " et pas des "=" qu'il faut dans (**).
" et pas des "=" qu'il faut dans (**).
On a bien :




Donc convient.
convient.
On a bien :
Donc
Pseudo modifié : anciennement Trident2.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
