Complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 13:02
par Maths-ForumR » 18 Oct 2014, 13:02
Bonjour, voici mon problème :
Le plan est rapporté à un repère orthonormé R=(O, e1,e2) identifié au plan complexe.
On pose ;)=e^(2i;)/5) ; ;)=;)+;)^4 ; b=;)²+;)^3
1) a- Déterminer une équation du 2nd degrés (E) donc a et b sont les solutions.
1) b- En déduire les valeurs exactes de cos (2;)/5) et cos(4;)/5).
Pour avoir 2 solution il fut que ;)=b²-4ac >0
Mais je ne vois pas comment faire.
Merci d'avance
-
mathelot
 par mathelot » 18 Oct 2014, 13:17
par mathelot » 18 Oct 2014, 13:17
bonjour,
quand tu fais
a+b+1
tu obtiens la somme de cinq termes d'une progression géométrique
quand tu calcule le produit
ab
tu as des puissances de

que tu peux réduire modulo 5 car

ces remarques devraient te permettre de calculer a+b et ab
et d'obtenir a et b comme racines d'un trinome du second degré.
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 13:22
par Maths-ForumR » 18 Oct 2014, 13:22
Merci pour la réponse !
Juste pourquoi ajouter 1 à a+b car la suite commence a 1 ?
-
mathelot
 par mathelot » 18 Oct 2014, 13:27
par mathelot » 18 Oct 2014, 13:27
oui:::::::::
-
mathelot
 par mathelot » 18 Oct 2014, 13:32
par mathelot » 18 Oct 2014, 13:32
le passage délicat est à la fin.
tu exprimes a et b sous forme trigonométrique
tu as calculé

disons
faut identifier

et
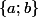
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 13:51
par Maths-ForumR » 18 Oct 2014, 13:51
Désolé mais je n'y arrive pas en cours on a fais un exo type avec U4 donc on pouvait le décomposer en produit de 2 carré et obtenir facilement les racine mais ici avec le facteur 5 cette méthode ne marche pas ...
-
mathelot
 par mathelot » 18 Oct 2014, 14:23
par mathelot » 18 Oct 2014, 14:23
réduis

développe :we:
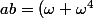(\omega^2+\omega^3)=.....=)
(développer et réduire via

)
-
mathelot
 par mathelot » 18 Oct 2014, 14:25
par mathelot » 18 Oct 2014, 14:25
^5=e^{2 i \pi}=1)
ça permet de réduire les puissances modulo 5 .
-
mathelot
 par mathelot » 18 Oct 2014, 14:29
par mathelot » 18 Oct 2014, 14:29
une fois que tu as calculé
a+b
et
ab
écrire
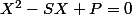
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 14:51
par Maths-ForumR » 18 Oct 2014, 14:51
Pour la somme j'ai :
(1+a+b) = 1 + e^(2i;)/5) + e^(4i;)/5) + e^(6i;)/5) +e^(8i;)/5)
(1+a+b) = 1 + [ e^(2i;)/5) + e^(4i;)/5) + e^(-4i;)/5) +e^(-2i;)/5) ]
(1+a+b) = 1 + 1 =
Pour le produit je trouve 1
c''est exacte ?
-
mathelot
 par mathelot » 18 Oct 2014, 15:07
par mathelot » 18 Oct 2014, 15:07
réduire les arguments modulo

sinon, tu peux travailler avec les littéraux,

^n=e^{i n \theta})
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 15:08
par Maths-ForumR » 18 Oct 2014, 15:08
Oui je viens de voir la simplifiction donc
Pour la somme j'ai :
(1+a+b) = 1 + e^(2i;)/5) + e^(4i;)/5) + e^(6i;)/5) +e^(8i;)/5)
(1+a+b) = 1 + [ e^(2i;)/5) + e^(4i;)/5) + e^(-4i;)/5) +e^(-2i;)/5) ]
(1+a+b) = 1 + 1 =2
Pour le produit je trouve 1
c''est exacte ?
-
mathelot
 par mathelot » 18 Oct 2014, 15:11
par mathelot » 18 Oct 2014, 15:11
Maths-ForumR a écrit:Oui je viens de voir la simplifiction donc
(1+a+b) = 1 + [ e^(2i;)/5) + e^(4i;)/5) + e^(-4i;)/5) +e^(-2i;)/5) ]
(1+a+b) = 1 + 1
pas compris.
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 15:13
par Maths-ForumR » 18 Oct 2014, 15:13
e^(6i;)/5) = e^(-4i;)/5)
e^(8i;)/5) = e^(-2i;)/5)
Donc si on additionne e^(2i;)/5) + e^(4i;)/5) + e^(-4i;)/5) +e^(-2i;)/5) ça nous donne 1.
Donc on obtient 2.
-
mathelot
 par mathelot » 18 Oct 2014, 15:15
par mathelot » 18 Oct 2014, 15:15
non, ça donne
-2cos(\frac{\pi}{5}))
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 15:32
par Maths-ForumR » 18 Oct 2014, 15:32
Ah oui pardon donc :
(1+a+b) = 1 + 2cos(2;)/5) + 2cos(4;)/5)
et
ab = w^3 +w^4 + w^6 + w^7
ab = w^5 ( w^-2 + w^-1 + w + w²)
ab = 1 [ e^(-4i;)/5) + e^(-2i;)/5) + e^(2i;)/5) + e^(4i;)/5) ]
ab = 2cos(2;)/5) + 2cos(4;)/5) ? j'ai un doute sur le résultat
-
mathelot
 par mathelot » 18 Oct 2014, 15:38
par mathelot » 18 Oct 2014, 15:38
combien vaut

?
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 18 Oct 2014, 15:43
par Maths-ForumR » 18 Oct 2014, 15:43
Ah c'est la somme des terme de la suite géométrique Q^n donc 0
-
mathelot
 par mathelot » 18 Oct 2014, 15:49
par mathelot » 18 Oct 2014, 15:49
oui,
1+a+b=0
donc a+b=
développer et réduire le produit ab.
-
mathelot
 par mathelot » 18 Oct 2014, 15:58
par mathelot » 18 Oct 2014, 15:58
.....................
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
