Complexe en géométrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 03 Jan 2007, 13:04
par max59 » 03 Jan 2007, 13:04
Bonjour,
J'ai quelques difficultées sur l'exercice suivant sur les complexes:
****
Le plan complexe est rapporté a un repere orthonormal direct (0, u, v)
A tout point m, on associe le point M d'affixe Z avec Z=1/(z^2) et on note z=r.e^i.téta
1)
soit l'équation Z0=1/z0^2
est-il possible de trouver z0, si oui z0 est-il unique?
2)
si module (z)=1 et arg(z)=téta
Que vaut arg(Z)?
3)
Quels sont les points m pour lesquels module(z)=1 et Z=z ?
4)
Soit d* une demi-droite d'origine O privée de O
Si m décrit d*, Quel est l'ensemble des points M?
5)
Si M décrit d* de 4), Quel est alors l'ensemble des points m?
6)
Enfin, soit f la fonction qui a m associe M,
Quelle est la fonction de f?
******
Désolé pour ce mitraillage de questions ;) mais j'ai beaucoup de mal avec cette exercice
Merci pour votre aide :)
Max
-
mathelot
 par mathelot » 03 Jan 2007, 13:27
par mathelot » 03 Jan 2007, 13:27
Tout est dans la relation

il faut que tu répondes aux questions suivantes:
quel est l'argument de Z ? quel est le module de Z ?
tout découle de ça.
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 03 Jan 2007, 13:42
par max59 » 03 Jan 2007, 13:42
Pour moi arg Z = -2téta pour le reste ca ne me vient pas a l'esprit :hum:
-
mathelot
 par mathelot » 03 Jan 2007, 15:15
par mathelot » 03 Jan 2007, 15:15
donc
 = -2 \theta \quad (2\pi))
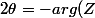 \quad (2\pi))
(R)
que peut on dire de module de Z ?
sais tu diviser les relations de congruence modulo

comme (R)
par 2 pour trouver

?
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 03 Jan 2007, 15:45
par max59 » 03 Jan 2007, 15:45
merci pour ton aide mathelot :we:
dsl tu vas me prendre pour un boulet mais je ne vois pas tres bien ou tu veux en venir...
Le module de Z est 1/r^2
La forme exponentielle de Z etant 1/r^2 e^(-2.i.téta)
f serait donc une rotation?
maintenant pour les question 3), 4), 5) je nage encore un peu :hum:
-
mathelot
 par mathelot » 03 Jan 2007, 16:49
par mathelot » 03 Jan 2007, 16:49
mathelot a écrit: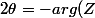 \quad (2\pi))
(R)
tu peux diviser la congruence par 2, ça donne une congruence modulo

donc
}{2})
modulo

soit deux valeurs possible pour

qui diffère de

donc deux nombres complexes pour z opposés.
-
mathelot
 par mathelot » 03 Jan 2007, 16:55
par mathelot » 03 Jan 2007, 16:55
question (3):
si module (z) =1 , que vaut module(Z) ?
si z=Z et
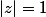
écris-moi une congruence avec arg(z) modulo (2

) dans ce cas là.
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 03 Jan 2007, 18:05
par max59 » 03 Jan 2007, 18:05
mathelot a écrit:question (3):
si module (z) =1 , que vaut module(Z) ?
si z=Z et
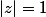
écris-moi une congruence avec arg(z) modulo (2

) dans ce cas là.
module(Z) est aussi égal a 1
et
arg(z)=téta [2pi]
Je remarque que les points m se situent sur un 1/4 cercle de centre O et de rayon 1
est-ce exact?

-
mathelot
 par mathelot » 03 Jan 2007, 19:10
par mathelot » 03 Jan 2007, 19:10
comme z=Z
arg(z)=arg(Z) (

)
d'où:
arg(z)=-2 arg(z) (

)
3 arg(z)=0 (

)
attention, on divise la congruence par 3:
arg(z)=0 (
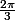
)
soit z=1 ou z=j ou z=
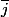
les racines cubiques de l'unité.
tchao.
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 03 Jan 2007, 19:26
par max59 » 03 Jan 2007, 19:26
au final ce sont les sommets d'un triangle equilateral;)
un grand merci pour ton aide :)
Je vais essayer de me debrouiller pour le reste ...
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 04 Jan 2007, 13:08
par max59 » 04 Jan 2007, 13:08
Dear Mathelot
concernant la question 4)
la reponse est -elle une droite ayant comme vecteur directeur u1 tel quel (u1,u) = 2.téta [2pi] ?
merci
-
max59
- Membre Naturel
- Messages: 26
- Enregistré le: 03 Jan 2007, 12:43
-
 par max59 » 05 Jan 2007, 16:28
par max59 » 05 Jan 2007, 16:28
Dear Mathelot
concernant la question 4)
la reponse est -elle une droite ayant comme vecteur directeur u1 tel quel (u1,u) = 2.téta [2pi] ?
merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
