Comparaison avec d'une série avec une série géométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptit_andrea65
- Membre Naturel
- Messages: 37
- Enregistré le: 03 Oct 2007, 06:42
-
 par ptit_andrea65 » 25 Nov 2007, 11:43
par ptit_andrea65 » 25 Nov 2007, 11:43
Bonjour je rencontre qq difficultés à résoudre une question , pourriez vous m'aider s'il vous plait !

Soit lxl < 1 et on pose
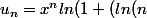/n^2/3 ))
En comparant lu_nl avec n dans N* à une suite géométrique, montrer que
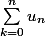
converge
On m' parlé du critère de d'alembert en divisant u_n+1 par u_n ... Mais je reste bloqué pourriez vous m'indiquer la marche à suivre ou si vous disposez d'une meilleure méthode .
Bien merci pour votre aide !!! :doh:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Nov 2007, 12:59
par fatal_error » 25 Nov 2007, 12:59
bonjour,
On a envie de majorer ln(bazzar) par 1
ln(bazzar)<1 qqsoit n?
ln(e)=1.
donc on a 1+ln(n)/3n²on en déduit qqsoit n ln(n)/3n²<1=>ln(bazzar)<1
L'intérêt de la série géométrique, c'est de pouvoir se passer des critères \o/
Donc tu etudis la série somme des un, avec un=x^n
C'est une série de terme géométrique x.
somme de 0 à N pour N fixé = (1-x^N)/(1-x)
Quand N tend vers l'infini, tu trouves 1/(1-x)
Concernant le critère de d'Alembert, j'ai un petit doute a cause de la valeur négative de x, après peut être qu'on peut...
la vie est une fête

-
ptit_andrea65
- Membre Naturel
- Messages: 37
- Enregistré le: 03 Oct 2007, 06:42
-
 par ptit_andrea65 » 25 Nov 2007, 14:54
par ptit_andrea65 » 25 Nov 2007, 14:54
Oui mais ça n'est pas
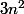
le dénominateur mais
)
est ce que cela change quelquechose ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Nov 2007, 14:58
par fatal_error » 25 Nov 2007, 14:58
lim ln/n^alpha = 0 en +l'infini, quelquesoit alpha>0
la vie est une fête

-
ptit_andrea65
- Membre Naturel
- Messages: 37
- Enregistré le: 03 Oct 2007, 06:42
-
 par ptit_andrea65 » 25 Nov 2007, 18:13
par ptit_andrea65 » 25 Nov 2007, 18:13
Je ne comprend pas... En effet la limite de la suite géométrique x^k est 1/1-x mais en quoi j'en déduis que la série de terme général u_n converge ? :triste:
De plus je n'ai pas comparé lu_nl à cette suite géo ? !!!

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Nov 2007, 18:37
par fatal_error » 25 Nov 2007, 18:37
qqsoit n, tu as Un qui est inférieur à x^n. Si la serie x^n converge, la serie Un aussi.
la vie est une fête

-
ptit_andrea65
- Membre Naturel
- Messages: 37
- Enregistré le: 03 Oct 2007, 06:42
-
 par ptit_andrea65 » 25 Nov 2007, 19:13
par ptit_andrea65 » 25 Nov 2007, 19:13
Oui mais a-ton lu_nl < x^k ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
