Comment résoudre ce système (3 équations, 4 inconnues) ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
RobTaku
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Oct 2009, 11:39
-
 par RobTaku » 27 Oct 2010, 12:54
par RobTaku » 27 Oct 2010, 12:54
Bonjour à tous,
J'ai un système d'équations qui doit me permettre de trouver un couple de solutions.
:\ \left{-x + y + 2z + 3t = 0 \\ 2z + 4t = 0 \\ -z - 2t = 0 \right)
Je trouve donc facilement que
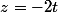
, mais comment conclure quelque chose pour x et y ?
Les systèmes d'équations ne sont vraiment pas mon fort, alors soyez indulgents s'il vous plait ._.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 27 Oct 2010, 13:00
par arnaud32 » 27 Oct 2010, 13:00
en realite les deux dernieres equations sont identiques
tu as donc deux equation, 4 inconnues
la base de tes solutions est donc de dim 2
tu as donc par exemple (y,z) en fonction de (x,t):
x=x
t=t
y=x+t
z=-2t
-
RobTaku
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Oct 2009, 11:39
-
 par RobTaku » 27 Oct 2010, 13:14
par RobTaku » 27 Oct 2010, 13:14
Hum, je suis pas sûr d'avoir compris..
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 27 Oct 2010, 13:24
par arnaud32 » 27 Oct 2010, 13:24
tu ne peux pas trouver une solution unique.
tu peux juste parametrer tes solutions. ici j'ai choisi t et x en parametres.
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 27 Oct 2010, 14:41
par JeanJ » 27 Oct 2010, 14:41
salut RobTaku,
La réponse t'a été donnée par Arnaud32 :
y=x+t
z=-2t
Ensuite, tu peux te donner n'importe quelles valeurs pour x et t.
Par exemple , si tu te donnes x=127 et t = 21
y = 127+21 = 148
z = -2*21 = -42
et tu as obtenu une solution de ton système : (x=127, y=148, z=-42, t=21)
Come cela tu peux calculer autant de solutions différentes que tu veux.
-
RobTaku
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Oct 2009, 11:39
-
 par RobTaku » 27 Oct 2010, 14:50
par RobTaku » 27 Oct 2010, 14:50
D'accord, je comprends mieux merci ! J'avais en effet besoin d'un exemple pour bien cerner le problème ><
Merci encore !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités