Résoudre système à n inconnues

par **Zweig** » 04 Avr 2010, 20:04

Salut,

J'aimerai résoudre le système suivant, où les

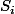
sont les inconnues et les

des rationnels donnés.

Avez-vous un site où je peux résoudre, dans le cas général, de tels systèmes ? Car j'ai un peu la flemme de le faire à la main :we: Le système est celui formé lorsque p varie de 1 à n :

Merci d'avance.

par **busard_des_roseaux** » 04 Avr 2010, 20:38

il ne serait pas triangulaire , par hasard ?

par **Zweig** » 19 Juin 2010, 15:41

Je réitère. Quelqu'un peut-il résoudre pour moi ce système d'équations via Maple (ou autre), car je ne l'ai pas :cry:

par **windows7** » 19 Juin 2010, 15:50

c'est un truc d'analyse numerique ?

par **Zweig** » 19 Juin 2010, 15:55

C'est-à-dire ?

par **windows7** » 19 Juin 2010, 16:03

ca me fait penser a du newton-cotes fermé ..

par **Zweig** » 19 Juin 2010, 16:07

Les relations viennent en effet de la relation coefficients-racines de Newton. J'ai généralisé une méthode pour mon TIPE du calcul de

par la méthode d'un mathématicien amateur grec au calcul de

, j'ai montré que

, il me manque plus qu'à expliciter cette constante C en fonction des nombres de Bernoulli. Pour ça, il me faut résoudre ce système.

par **windows7** » 19 Juin 2010, 16:12

d'accord

tu peux ecrire de facon plus lisible ton equation ?

Résoudre système à n inconnues

Résoudre système à n inconnues

Qui est en ligne