bonjour,
quelqu'un peut m'éclairer sur la cohomologie ?
est ce que l'on forme des groupes à partir de suites exactes, courtes ou longues
est ce que la non trivialité de ces groupes mesure une obstruction ?
si oui, laquelle ?
peut on avoir un exemple de calcul ?
merci.
Cohomologie
10 messages
- Page 1 sur 1
Bonjour,
La cohomologie c'est essentiellement comprendre la topologie d'un espace de manière combinatoire. Ca peut prendre plein de formes plus ou moins sophistiquées, mais l'idée de base c'est celle là (meme sous ses avatars plus algébriques, comme la cohomologie galoisienne, on peut se rattacher à cette intuition).
Il faut donc deux choses, des "ouverts" (ou tout du moins qqch qui joue le role d'ouverts) et des "objets" au dessus de ces ouverts, avec la possibilité de les recoller sur les intersections de ces ouverts. La (co)homologie mesure les obtructions à recoller les objets definis localement.
La cohomologie la plus importante en topologie et en geometrie est la cohomologie singulière ou de Betti. En fait on essaie a peu pres toujours de modéliser les propriétés d'un theorie cohomologie que celle ci (meme si parfois on relache certaines propriétés, comme par exemple les théories cohomologiques dites extraordinaires). Elle donne de bons objets pour des espaces localement contractiles donc par exemple toutes les variétés topologiques.
L'abstraction de ce que j'ai dit plus haut mène à la cohomologie des faisceaux.
Pour répondre autre chose, il faudrait des questions plus precises.
La cohomologie c'est essentiellement comprendre la topologie d'un espace de manière combinatoire. Ca peut prendre plein de formes plus ou moins sophistiquées, mais l'idée de base c'est celle là (meme sous ses avatars plus algébriques, comme la cohomologie galoisienne, on peut se rattacher à cette intuition).
Il faut donc deux choses, des "ouverts" (ou tout du moins qqch qui joue le role d'ouverts) et des "objets" au dessus de ces ouverts, avec la possibilité de les recoller sur les intersections de ces ouverts. La (co)homologie mesure les obtructions à recoller les objets definis localement.
La cohomologie la plus importante en topologie et en geometrie est la cohomologie singulière ou de Betti. En fait on essaie a peu pres toujours de modéliser les propriétés d'un theorie cohomologie que celle ci (meme si parfois on relache certaines propriétés, comme par exemple les théories cohomologiques dites extraordinaires). Elle donne de bons objets pour des espaces localement contractiles donc par exemple toutes les variétés topologiques.
L'abstraction de ce que j'ai dit plus haut mène à la cohomologie des faisceaux.
Pour répondre autre chose, il faudrait des questions plus precises.
https://www.youtube.com/watch?v=YNBi4Ix3cY0
si tu es à l'aise en anglais, tu trouveras peut-être des éléments de réponse à tes questions dans ces vidéos (ça commence à la vidéo 30, mais celle-ci est peut-être la plus instructive).
si tu es à l'aise en anglais, tu trouveras peut-être des éléments de réponse à tes questions dans ces vidéos (ça commence à la vidéo 30, mais celle-ci est peut-être la plus instructive).
Bon j'en profite pour etoffer un peu ma reponse.
Donc comme je le disais, l'homologie et sa duale la cohomologie, ont pour but de comprendre de manière combinatoire une situation topologique. Il est bien sur vain d'esperer comprendre n'importe quel espace topologique, qui peuvent etre trop eloignés de l'intuition géométrique. Pour cela on regarde en general des classes de sous espaces plus gentils.
Un complexe simplicial est la donnée d'une liste de points et d'une liste de sous ensemble de ces points qui soit stable par sous ensemble. Il faut penser à ces points comme à des points dans l'espace et à la liste de sous ensembles comme a des simplexes battis sur ces points que l'on adjoint aux points (un segment, un triangle, un tetraèdre sont des exemples de simplexes plus generalement le n-simplexe c'est l'ensemble des (x0,...,xn) tels que la somme des x_i vallent 1 et que tous les x_i soient entre 0 et 1). A la donnée d'un tel complexe simplicial on peut associer deux choses.
Une realisation, qui est un espace topologique, qui est batti comme j'ai dit plus haut, on prend des points, et on adjoint inductivement les simplexes accordément à la liste de simplexes. Par exemple donne un triangle plein, alors que donne un triangle (seulement les aretes donc). On peut donc associer à un complexe simplicial abstrait un espace topologique (je n'ai pas dit comment on mettait la topologie).
On peut aussi lui associer un complexe de chaines, de la manière suivante.
On pose=\oplus Z \Delta^X_q) le groupe abélien libre engendré par tous les q-simplexes que l'on a dans la definition du complexe simplicial X pour le triangle plein par exemple C_2 consiste en le groupe libre engendré par l'unique 2 simplexe, C_2 c'est Z^3, avec un generateur par arretes etc... Mais il y a bien sur plus de structure que cela sur C(X). A n'importe quel simplexe, on peut lui associer son bord qui est une somme formelle de simplexes par exemple le bord du 2-simplexe, le triangle plein, est la somme alternée des 1 simplexes en formant les arretes. Comme la liste de simplexes dans X est stable par sous ensemble on obtient une application
le groupe abélien libre engendré par tous les q-simplexes que l'on a dans la definition du complexe simplicial X pour le triangle plein par exemple C_2 consiste en le groupe libre engendré par l'unique 2 simplexe, C_2 c'est Z^3, avec un generateur par arretes etc... Mais il y a bien sur plus de structure que cela sur C(X). A n'importe quel simplexe, on peut lui associer son bord qui est une somme formelle de simplexes par exemple le bord du 2-simplexe, le triangle plein, est la somme alternée des 1 simplexes en formant les arretes. Comme la liste de simplexes dans X est stable par sous ensemble on obtient une application 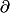 de C_q(X) dans C_{q-1}(X) qui est bien définie, et qui verifie
de C_q(X) dans C_{q-1}(X) qui est bien définie, et qui verifie 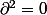 comme on le verifie aisément.
comme on le verifie aisément.
Cela implique que le noyau du bord contient l'image du bord et le quotient du premier par le dernier donne un groupe, que l'on appelle le q-ième groupe d'homologie du complexe simplicial X.
Cette définition est extremement pratique pour les calculs. Elle permet de calculer les groupes d'homologies des complexes simpliciaux. Mais elle souffre de beaucoup de problemes.
Nous ce qu'on veut c'est comprendre la topologie d'un espace X. Mais la ce qu'on étudie, c'est la donnée d'une triangulation d'un espace X, et en fait pire, on se donne la triangulation avant l'espace. Il faut donc s'assurer que ce qu'on obtient, les groupes d'homologie en question, ne dependent pas de la triangulation choisie si par exemple on décide de rafiner la triangluation (d'ajouter des simplexes, par exemple, je peux prendre le tetraedre classique, et sous trianguler une de ces faces en ajoutant un sommet, le barycentre de la face en question, est ce que ca change l'homologie?) et meme de la classe d'homeomorphisme de l'espace que l'on obtient par realisation.
On peut attaquer le probleme bille en tete, mais on se heurte à certaines difficultés dont certaines ne peuvent pas etre contournées. Par exemple on peut démontrer que si l'on se donne une realisation d'un complexe simplicial et qu'on raffine la triangulation, on ne change pas l'homologie associée. Par contre, on sait que si l'on se donne un espace quelconque, et deux triangulations de celui ci, il ne sera pas possible en general, des que la dimension de l'espace est plus grande que 3 (i.e il contient au moins un 3-simplexe) de trouver une triangulation qui soit un raffinement commun des deux, c'est le Hauptvermutung.
Pour résoudre toutes ces difficultés, le moyen le plus simple est d'introduire la cohomologie singulière. C'est une définition bien plus compliquée et generale de la cohomologie d'un espace, qui est impossible à calculer en pratique (enfin, directement à partir des definitions), mais qui est beaucoup plus facile à manipuler de manière abstraite. Ensuite on démontre que les groupes d'homologies singulières, qui eux ne dependent que, de manière tautologique au vu de leur définition, de la classe d'homemorphisme (et meme beaucoup moins que ca) de l'espace en question, sont les memes que les groupes d'homologie simpliciale définie au moyen de triangulations.
Donc pour calculer l'homologie d'un espace, on essaie d'en trouver une triangulation, c'est à dire un homéo avec la realisation d'un complexe simplicial, et on calcule ensuite l'homologie du complexe simplicial qu'on a trouvé, sachant qu'on est assuré que rien ne va dépendre des choix qu'on fait.
ON peut alors facilement calculer l'homologie du tore, de la sphere etc...
Voila pour le debut de l'histoire.
Donc comme je le disais, l'homologie et sa duale la cohomologie, ont pour but de comprendre de manière combinatoire une situation topologique. Il est bien sur vain d'esperer comprendre n'importe quel espace topologique, qui peuvent etre trop eloignés de l'intuition géométrique. Pour cela on regarde en general des classes de sous espaces plus gentils.
Un complexe simplicial est la donnée d'une liste de points et d'une liste de sous ensemble de ces points qui soit stable par sous ensemble. Il faut penser à ces points comme à des points dans l'espace et à la liste de sous ensembles comme a des simplexes battis sur ces points que l'on adjoint aux points (un segment, un triangle, un tetraèdre sont des exemples de simplexes plus generalement le n-simplexe c'est l'ensemble des (x0,...,xn) tels que la somme des x_i vallent 1 et que tous les x_i soient entre 0 et 1). A la donnée d'un tel complexe simplicial on peut associer deux choses.
Une realisation, qui est un espace topologique, qui est batti comme j'ai dit plus haut, on prend des points, et on adjoint inductivement les simplexes accordément à la liste de simplexes. Par exemple donne un triangle plein, alors que donne un triangle (seulement les aretes donc). On peut donc associer à un complexe simplicial abstrait un espace topologique (je n'ai pas dit comment on mettait la topologie).
On peut aussi lui associer un complexe de chaines, de la manière suivante.
On pose
Cela implique que le noyau du bord contient l'image du bord et le quotient du premier par le dernier donne un groupe, que l'on appelle le q-ième groupe d'homologie du complexe simplicial X.
Cette définition est extremement pratique pour les calculs. Elle permet de calculer les groupes d'homologies des complexes simpliciaux. Mais elle souffre de beaucoup de problemes.
Nous ce qu'on veut c'est comprendre la topologie d'un espace X. Mais la ce qu'on étudie, c'est la donnée d'une triangulation d'un espace X, et en fait pire, on se donne la triangulation avant l'espace. Il faut donc s'assurer que ce qu'on obtient, les groupes d'homologie en question, ne dependent pas de la triangulation choisie si par exemple on décide de rafiner la triangluation (d'ajouter des simplexes, par exemple, je peux prendre le tetraedre classique, et sous trianguler une de ces faces en ajoutant un sommet, le barycentre de la face en question, est ce que ca change l'homologie?) et meme de la classe d'homeomorphisme de l'espace que l'on obtient par realisation.
On peut attaquer le probleme bille en tete, mais on se heurte à certaines difficultés dont certaines ne peuvent pas etre contournées. Par exemple on peut démontrer que si l'on se donne une realisation d'un complexe simplicial et qu'on raffine la triangulation, on ne change pas l'homologie associée. Par contre, on sait que si l'on se donne un espace quelconque, et deux triangulations de celui ci, il ne sera pas possible en general, des que la dimension de l'espace est plus grande que 3 (i.e il contient au moins un 3-simplexe) de trouver une triangulation qui soit un raffinement commun des deux, c'est le Hauptvermutung.
Pour résoudre toutes ces difficultés, le moyen le plus simple est d'introduire la cohomologie singulière. C'est une définition bien plus compliquée et generale de la cohomologie d'un espace, qui est impossible à calculer en pratique (enfin, directement à partir des definitions), mais qui est beaucoup plus facile à manipuler de manière abstraite. Ensuite on démontre que les groupes d'homologies singulières, qui eux ne dependent que, de manière tautologique au vu de leur définition, de la classe d'homemorphisme (et meme beaucoup moins que ca) de l'espace en question, sont les memes que les groupes d'homologie simpliciale définie au moyen de triangulations.
Donc pour calculer l'homologie d'un espace, on essaie d'en trouver une triangulation, c'est à dire un homéo avec la realisation d'un complexe simplicial, et on calcule ensuite l'homologie du complexe simplicial qu'on a trouvé, sachant qu'on est assuré que rien ne va dépendre des choix qu'on fait.
ON peut alors facilement calculer l'homologie du tore, de la sphere etc...
Voila pour le debut de l'histoire.
Bon, je reprend mon monologue.
J'ai dit un petit mot de l'homologie simpliciale et ait precisé qu'elle calcule la meme chose que l'homologie singulière bien que cette dernière soit plus facile à manipuler pour faire des preuves generales. Me reste à décrire un peu ce qu'est l'homologie singulière et surtout à dire ce qu'est la cohomologie, et pourquoi est ce un outil plus fin et plus puissant que l'homologie.
L'homologie singulière.
L'homologie singulière se définit un peu de la meme manière que la simpliciale, mais au lieu de se limiter pour les C_q aux simplexes definis par une triangulation explicite, on ne se limite à... rien. Un simplexe singulier est une application continue du q-simplexe standard dans X. C_q,sing(X) est le (monstrueux) groupe abélien libre bati sur les q-simplexes singuliers de X, on peut définir de la meme facon le bord d'un simplexe singulier que dans le cas simpliciale, et de la meme manière on a un complexe de groupes abéliens i.e\leftarrow^\partial C_{1,sing}(X) ...) avec
avec 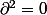
On a d'autre part pour tout choix d'une triangulation de X (quand c'est possible), donc d'un homéo de X avec la realisation d'un complexe simplicial, une inclusion du complexe simplicial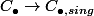 définie par le fait qu'un simplexe de la triangluation est un simplexe singulier, et que l'operateur bord est preservé.
définie par le fait qu'un simplexe de la triangluation est un simplexe singulier, et que l'operateur bord est preservé.
Comme je l'ai dit plus haut cette application est un quasi-isomorphisme, c'est à dire qu'elle induit un isomorphisme sur les groupes d'homologies (le fait de commuter avec le bord implique comme on le voit immediatement que l'application définie plus haut, induit un morphisme sur les groupes d'homologies).
L'avantage de l'homologie singluière c'est que deja elle permet d'introduire un peu de fonctorialité dans le tableau. Si f est une application de X dans Y (continue bien sur) alors un simplexe singulier de X est mappé par f sur un simplexe singulier de Y par composition (ce qui n'est bien sur pas du tout le cas dans le cas simplicial si l'application f n'est pas simpliciale, terme que je ne vais pas définir mais qui s'intuite assez bien). Il est tout aussi facile de s'apercevoir que l'application entre complexes que l'on obtient (du complexe singulier de X dans celui de Y) commute au bord, et induit donc une application entre les groupes d'homologies. Cette application est fonctorielle i.e l'application définie par une composition d'applications continues et la composée des application entre les complexes et de facto entre l'homologie.
Ce petit fait permet deja de prouver des theoremes de topologie. Comme l'invariance du domaine de Brouwer, ou meme le theoreme du point fixe de Brouwer également.
Au passage, une fois qu'on a démontré des theoremes de finitude adéquat (dans ce que j'ai dit plus haut rien n'indique que les groupes d'homologies singulières soient de rang fini, alors que c'est évident pour les groupes d'homologies simpliciales des que le complexe simplicial est compact), on peut définir des choses comme la carractéristique d'Euler Poincaré d'un espace, qui eclaire certains fait classiques. Par exemple pour un polyèdre de dimension 2, il est assez facile de se convaincre que la formule S-A+F (nombre de sommets-nombre de arretes+nombre de faces) est exactement la somme alternée des rangs des groupes de chaines simpliciales. C'est un petit exercice de prouver que cette somme alternée est exactement la somme alternée des rangs des groupes d'homologie... et donc ne dépend pas de la triangulation!
La cohomologie.
La difference entre la cohomologie (singulière ici) et l'homologie peut se résumer en un seul mot: produit.
Il est possible de définir naturellement sur la cohomologie une structure d'anneau (gradué) alors que ca n'est pas possible en general sur l'homologie (sauf artefact).
Le complexe des cochaines singulières d'un espace X, est le complexe des duaux (dans Z) des groupes de chaines singulières, muni des transposées des applications bords. Bien sur, il va du coup dans l'autre sens.\to^\partial C^{1,sing}(X) ...)
Une cochaine singulière est une fonction \to \mathbb Z) qui soit linéaire. C'est la donnée d'un nombre entier pour tout simplexe singulier de X (pas plus pas moins).
qui soit linéaire. C'est la donnée d'un nombre entier pour tout simplexe singulier de X (pas plus pas moins).
On peut définir, pour s et t, deux cochaines singulières (de degré q et q'), leur (cup-)produit s.t de degré q+q', qui doit donc donner une nombre pour tout q+q' simplexe singulier de X. Le q+q' simplexe standard, a une première (une fois choisie une numérotation adéquate) q-face et une q' face opposée (dans un tetraedre la 1-face opposée à une 2-face est l'unique sommet qui ne la touche pas etc...), on peut donc associer à s et t, et un q+q'-simplexe singulier le produit de la valeur associée par s sur la première q-face et de la valeur associée par t sur la q'-face opposée.
On obtient donc un produit s.t, dont il est tautologique de verifier qu'il verifie (je note d au lieu de \partial l'operateur cobord) d(s.t)=ds.t+(-1)^q' s.dt, et donc ce produit passe à la cohomologie.
Cette structure de produit sur la cohomologie est un des ingrédient les plus fondamentaux de la géométrie. On peut en donner une interpretation géométrique liée à la notion d'intersection. Il permet par exemple de faire la difference entre une fibration non triviale et un simple produit (la fibration de Hopf a des groupes de cohomologie isomorphes à ceux de la fibration triviale entre la 2 et la 1-sphère, mais pas la meme algèbre de cohomologie).
Il me faudrait beaucoup plus de place pour expliquer pourquoi cette structure est fondamentale. POur donner une idée, je peux simplement mentionner qu'en une certain sens, la classification des surfaces complexes compactes est basée uniquement sur les propriétés de ce produit.
On peut mettre en lumière d'autre structures sur la cohomologie qui permettent de montrer son interet et dans lequel j'ai pas trop le temps de me lancer (lien avec les points fixes, liens avec la notion de courbure, de singularités, dualité de Poincaré, formule de Kunneth, suite exacte de Mayer-Vietoris), dont je parlerais peut etre une autre fois. Mais je voudrais simplement rajouter qu'essentiellement toutes les autres theories cohomologies, tentent d'importer ce cadre de la cohomologie singulière (des variétés topologiques) a des domaines où elle ne s'applique pas directement (pour diverses raisons). C'est le cas des cohomologies sophistiquées introduites bien apres (étale, l-adiques, cyclique, cristalline etc...).
J'ai dit un petit mot de l'homologie simpliciale et ait precisé qu'elle calcule la meme chose que l'homologie singulière bien que cette dernière soit plus facile à manipuler pour faire des preuves generales. Me reste à décrire un peu ce qu'est l'homologie singulière et surtout à dire ce qu'est la cohomologie, et pourquoi est ce un outil plus fin et plus puissant que l'homologie.
L'homologie singulière.
L'homologie singulière se définit un peu de la meme manière que la simpliciale, mais au lieu de se limiter pour les C_q aux simplexes definis par une triangulation explicite, on ne se limite à... rien. Un simplexe singulier est une application continue du q-simplexe standard dans X. C_q,sing(X) est le (monstrueux) groupe abélien libre bati sur les q-simplexes singuliers de X, on peut définir de la meme facon le bord d'un simplexe singulier que dans le cas simpliciale, et de la meme manière on a un complexe de groupes abéliens i.e
On a d'autre part pour tout choix d'une triangulation de X (quand c'est possible), donc d'un homéo de X avec la realisation d'un complexe simplicial, une inclusion du complexe simplicial
Comme je l'ai dit plus haut cette application est un quasi-isomorphisme, c'est à dire qu'elle induit un isomorphisme sur les groupes d'homologies (le fait de commuter avec le bord implique comme on le voit immediatement que l'application définie plus haut, induit un morphisme sur les groupes d'homologies).
L'avantage de l'homologie singluière c'est que deja elle permet d'introduire un peu de fonctorialité dans le tableau. Si f est une application de X dans Y (continue bien sur) alors un simplexe singulier de X est mappé par f sur un simplexe singulier de Y par composition (ce qui n'est bien sur pas du tout le cas dans le cas simplicial si l'application f n'est pas simpliciale, terme que je ne vais pas définir mais qui s'intuite assez bien). Il est tout aussi facile de s'apercevoir que l'application entre complexes que l'on obtient (du complexe singulier de X dans celui de Y) commute au bord, et induit donc une application entre les groupes d'homologies. Cette application est fonctorielle i.e l'application définie par une composition d'applications continues et la composée des application entre les complexes et de facto entre l'homologie.
Ce petit fait permet deja de prouver des theoremes de topologie. Comme l'invariance du domaine de Brouwer, ou meme le theoreme du point fixe de Brouwer également.
Au passage, une fois qu'on a démontré des theoremes de finitude adéquat (dans ce que j'ai dit plus haut rien n'indique que les groupes d'homologies singulières soient de rang fini, alors que c'est évident pour les groupes d'homologies simpliciales des que le complexe simplicial est compact), on peut définir des choses comme la carractéristique d'Euler Poincaré d'un espace, qui eclaire certains fait classiques. Par exemple pour un polyèdre de dimension 2, il est assez facile de se convaincre que la formule S-A+F (nombre de sommets-nombre de arretes+nombre de faces) est exactement la somme alternée des rangs des groupes de chaines simpliciales. C'est un petit exercice de prouver que cette somme alternée est exactement la somme alternée des rangs des groupes d'homologie... et donc ne dépend pas de la triangulation!
La cohomologie.
La difference entre la cohomologie (singulière ici) et l'homologie peut se résumer en un seul mot: produit.
Il est possible de définir naturellement sur la cohomologie une structure d'anneau (gradué) alors que ca n'est pas possible en general sur l'homologie (sauf artefact).
Le complexe des cochaines singulières d'un espace X, est le complexe des duaux (dans Z) des groupes de chaines singulières, muni des transposées des applications bords. Bien sur, il va du coup dans l'autre sens.
Une cochaine singulière est une fonction
On peut définir, pour s et t, deux cochaines singulières (de degré q et q'), leur (cup-)produit s.t de degré q+q', qui doit donc donner une nombre pour tout q+q' simplexe singulier de X. Le q+q' simplexe standard, a une première (une fois choisie une numérotation adéquate) q-face et une q' face opposée (dans un tetraedre la 1-face opposée à une 2-face est l'unique sommet qui ne la touche pas etc...), on peut donc associer à s et t, et un q+q'-simplexe singulier le produit de la valeur associée par s sur la première q-face et de la valeur associée par t sur la q'-face opposée.
On obtient donc un produit s.t, dont il est tautologique de verifier qu'il verifie (je note d au lieu de \partial l'operateur cobord) d(s.t)=ds.t+(-1)^q' s.dt, et donc ce produit passe à la cohomologie.
Cette structure de produit sur la cohomologie est un des ingrédient les plus fondamentaux de la géométrie. On peut en donner une interpretation géométrique liée à la notion d'intersection. Il permet par exemple de faire la difference entre une fibration non triviale et un simple produit (la fibration de Hopf a des groupes de cohomologie isomorphes à ceux de la fibration triviale entre la 2 et la 1-sphère, mais pas la meme algèbre de cohomologie).
Il me faudrait beaucoup plus de place pour expliquer pourquoi cette structure est fondamentale. POur donner une idée, je peux simplement mentionner qu'en une certain sens, la classification des surfaces complexes compactes est basée uniquement sur les propriétés de ce produit.
On peut mettre en lumière d'autre structures sur la cohomologie qui permettent de montrer son interet et dans lequel j'ai pas trop le temps de me lancer (lien avec les points fixes, liens avec la notion de courbure, de singularités, dualité de Poincaré, formule de Kunneth, suite exacte de Mayer-Vietoris), dont je parlerais peut etre une autre fois. Mais je voudrais simplement rajouter qu'essentiellement toutes les autres theories cohomologies, tentent d'importer ce cadre de la cohomologie singulière (des variétés topologiques) a des domaines où elle ne s'applique pas directement (pour diverses raisons). C'est le cas des cohomologies sophistiquées introduites bien apres (étale, l-adiques, cyclique, cristalline etc...).
EGA-SGA a écrit:Bon, je reprend mon monologue.
... que je suis attentivement pour ma part. Petites questions (tu n'es pas forcé d'y répondre maintenant si tu as prévu de dire autre chose) :
1) Est-ce qu'il y a un lien avec les homologies/cohomologies définies par des foncteurs dérivés, genre cohomologie des faisceaux ?
2) En gros les h/ch singulières vont être utiles pour dire des choses sur les espaces qui ont une topologie qui ressemble "localement" à celle de R usuelle (simple connexité, groupe fondamental,...) mais pour une topologie de Zariski ça n'est plus valable... qu'est-ce qui va être valable du coup ?
L.A. a écrit:
1) Est-ce qu'il y a un lien avec les homologies/cohomologies définies par des foncteurs dérivés, genre cohomologie des faisceaux ?
Oui, il y a un lien.
La cohomologie singulière calcule la cohomologie à valeur dans le faisceau constant Z. La théorie des faisceaux a permis de comprendre que les differentes theories cohomologiques, avec leurs differents complexes et leurs differents coefficients n'etait en fait que des moyens explicites de calculer la cohomologie à coéfficient dans un faisceau. Si la cohomologie de de Rahm, la cohomologie singulière à coff réels, la cohomologie simpliciale etc... sont toutes la meme, c'est parce qu'a chaque fois on calcule qu'une seule chose, c'est la cohomologie à valeur dans le faisceau R. C'est ca la raison profonde.
Pour calculer la cohomologie d'un faisceau, il faut se donner une resolution injective, ou flasque, ou meme acyclique d'un faisceau. C'est ce que faisaient les theories cohomologiques classiques, donner des resolutions (parfois differentes) d'un meme faisceau.
L.A. a écrit:2) En gros les h/ch singulières vont être utiles pour dire des choses sur les espaces qui ont une topologie qui ressemble "localement" à celle de R usuelle (simple connexité, groupe fondamental,...) mais pour une topologie de Zariski ça n'est plus valable... qu'est-ce qui va être valable du coup ?
La cohomologie singulière ne se limite pas à au variétés topologiques, elle est extremement utile sur la catégorie des CW-complexes.
On peut tout à fait définir la cohomologie des faisceaux pour des variétés algébriques (pour leur topologie de Zariski donc), l'ennuie c'est que la cohomologie des faisceaux ne donne pas les resultats auquels on s'attend pour tous les faisceaux et notamment les faisceaux constants ou localement constants, qui sont ceux qui entrent en jeu dans la cohomologie singulière. Par exemple la cohomologie de C^* à valeur dans le faisceau constant Z, ca dervait etre, d'apres ma réponse à ta première question, la cohomologie singulière de C^* à valeur dans Z, il devrait dont y avoir du H^1, et pourtant la cohomologie de C^* pour la topologie de Zariski dans le faisceau contant Z est... nulle!
C'est effectivement problématique, mais tous n'est pas si noir que ca, il y a une catégorie de faisceau pour laquelle la cohomologie (calculée à partir de la topologie de Zariski) donne ce qu'il faut. Ce sont les faisceaux cohérents.
Pour récuperer la cohomologie de Betti/singulière, pour des variétés algébriques, il faut ruser. Il faut accepter de considérer des ouverts qui ne sont pas de vrais ouverts. Si on défini une bonne classe d'"ouvert generalisés" (ce que l'on appelle une topologie de Grothendieck) et qu'on calcule la cohomologie d'un faisceau constant pour ces ouverts generalisés là, ce qui n'est pas plus difficile que pour les ouverts classiques, alors on obtient bien ce que l'on attendait.
EGA-SGA a écrit:
C'est effectivement problématique, mais tous n'est pas si noir que ca, il y a une catégorie de faisceau pour laquelle la cohomologie (calculée à partir de la topologie de Zariski) donne ce qu'il faut. Ce sont les faisceaux cohérents.
Pour récuperer la cohomologie de Betti/singulière, pour des variétés algébriques, il faut ruser.
C'est peut-être là ce que je ne comprends pas au fond... (moi en cohomologie, je ne sais pas "ruser" justement, je prends ce qu'on me donne et j'essaye de piger, bref...)
Prenons C^* et sa topologie naturelle, on applique la "recette" simpliciale, on remue le nez comme dans "Ma sorcière bien aimée" et pof ! il y a du H^1 parce qu'il y a un trou. Prenons maintenant C^* et sa topologie de Zariski, on applique la "recette" simpliciale, ou bien la "recette" faisceau constant Z, et pof ! plus rien. De mon point de vue, c'est normal puisque les topologie étant (très) différentes, on ne s'attend pas du tout à trouver le même résultat.
Du coup, on réinvente toute une nouvelle recette ou même plusieurs, qui vont nous dire des choses sur la topologie de Zariski. Du coup, chaque topologie va avoir ses propres recettes, et celles qui marchent pour l'une ne marchent pas pour les autres en général. Donc qu'est-ce qui nous dit que toutes ces recettes vont donner les "mêmes" outils dans une topologie ou dans une autre ? Est-ce qu'une h/ch qui donne un résultat donne forcément un résultat "intéressant" et comparable aux autres ? Comment est-ce qu'on sait qu'une nouvelle recette va améliorer une ancienne, la prolonger à un cadre plus large tout en gardant le même sens, en s'interprétant de la même manière ?
:hein:
J'ai pas trop le temps de repondre en detail là, je donne simplement un embryon de réponse
Ben si, il faudrait trouver le meme resultat. Et le fait qu'on ne le trouve pas, est justement ce qui fait que ca n'est pas satisfaisant. Le H1 de C^*, ca doit etre un truc de rang 1, sinon c'est que notre theorie n'est pas bonne.
Pour des variétés algébriques sur C ou sur des sous corps de C, on s'en fout un peu, car on pourrait travailler avec la topologie usuelle. C'est d'ailleurs ce qu'on fait tous les géomètres algébristes avant les années 60. On perd un peu mais pas beaucoup. Pour d'autre cas (les corps finis notamment) on peut pas faire ca, alors il faut bien reussier à definir une topologie qui donne les bons groupes. Quand on voit qu'elle donne la bonne chose sur C, alors c'est qu'elle a de bonnes chances de donner ce qu'il faut sur les corps finis.
L.A. a écrit:C'est peut-être là ce que je ne comprends pas au fond... (moi en cohomologie, je ne sais pas "ruser" justement, je prends ce qu'on me donne et j'essaye de piger, bref...)
Prenons C^* et sa topologie naturelle, on applique la "recette" simpliciale, on remue le nez comme dans "Ma sorcière bien aimée" et pof ! il y a du H^1 parce qu'il y a un trou. Prenons maintenant C^* et sa topologie de Zariski, on applique la "recette" simpliciale, ou bien la "recette" faisceau constant Z, et pof ! plus rien. De mon point de vue, c'est normal puisque les topologie étant (très) différentes, on ne s'attend pas du tout à trouver le même résultat.
Ben si, il faudrait trouver le meme resultat. Et le fait qu'on ne le trouve pas, est justement ce qui fait que ca n'est pas satisfaisant. Le H1 de C^*, ca doit etre un truc de rang 1, sinon c'est que notre theorie n'est pas bonne.
Pour des variétés algébriques sur C ou sur des sous corps de C, on s'en fout un peu, car on pourrait travailler avec la topologie usuelle. C'est d'ailleurs ce qu'on fait tous les géomètres algébristes avant les années 60. On perd un peu mais pas beaucoup. Pour d'autre cas (les corps finis notamment) on peut pas faire ca, alors il faut bien reussier à definir une topologie qui donne les bons groupes. Quand on voit qu'elle donne la bonne chose sur C, alors c'est qu'elle a de bonnes chances de donner ce qu'il faut sur les corps finis.
Bon j'ai un peu de temps, je peux étoffer ma derniere réponse. Au passage, j'ai donné un cours de topologie algébrique d'introduction à l'homologie ce semestre, si l'envie me prend de latexiser mes notes de cours (manuscrites) je les mettrai peut etre ici, si cela vous interesse.
Donc, je disais pour comprendre pourquoi la cohomologie des faisceaux ne donne pas le bon resultat calculée avec la topologie de Zariski, il faut comprendre ce qu'essayaient de faire les gens à l'époque.
Deja, les géomètres algébristes de l'epoque (Zariski, Lefshetz) travaillaient sur C, et utilisaient la topologie analytique. C'est dans ce cadre qu'il ont pu mettre au point des theoremes puissants. En particulier la formule des traces de Lefhsetz est l'un des outils sur lequel l'attention s'est cristalisé. Ce theoreme dit que le nombre de point de points fixes d'une application continue d'un complexe simplificial fini dans lui meme vaut la somme alternées des traces de l'action de l'application induite sur les H_i(X,Q) (ou les H^i(X,Q) ca revient au meme).
Ce theoreme etait important pour la stratégie de compréhension des conjectures de Weil qu'avait établi Grothendieck.
Mais il y avait bien sur d'autres resultats de nature plus geometrique, le theoreme de la section hyperplane de Lefshetz par exemple, ou le theoreme sur les classes (1,1) (de Lefshetz également), ou encore le theoreme de Lefshetz difficile (qui est un cousin du theoreme sur les sections hyperplanes). Bref on voulait une theorie cohomologique pour les variétés quelconques qui puisse nous permettre de disposer de ces theoremes sur un corps quelconques (et surtout un corps fini).
Il y avait d'autres contraintes, notamment on souhaitait disposer d'un bon theoreme de comparaison.
Bref toutes ces contraintes ont engendré la notion de cohomologie de Weil. Et la cohomologie des faisceaux n'est pas une cohomologie de Weil.
Une cohomologie de Weil pour les variétés algébriques est donné par la cohomologie étale. Et on savait (Grothendieck, Deligne et d'autres) que la simple existence d'une cohomologie de Weil pour les variétés algébriques sur les corps finis suffisait à prouver la quasi totalité des conjectures de Weil.
Il y a d'autres raisons a ne pas vouloir que le H^1 de C^* (ou de G_m en fait) soit nul. Par exemple si on veut une theorie des classes carracteristique, le fait que le H^1(C^*) soit non nul est assez crucial.
Donc, je disais pour comprendre pourquoi la cohomologie des faisceaux ne donne pas le bon resultat calculée avec la topologie de Zariski, il faut comprendre ce qu'essayaient de faire les gens à l'époque.
Deja, les géomètres algébristes de l'epoque (Zariski, Lefshetz) travaillaient sur C, et utilisaient la topologie analytique. C'est dans ce cadre qu'il ont pu mettre au point des theoremes puissants. En particulier la formule des traces de Lefhsetz est l'un des outils sur lequel l'attention s'est cristalisé. Ce theoreme dit que le nombre de point de points fixes d'une application continue d'un complexe simplificial fini dans lui meme vaut la somme alternées des traces de l'action de l'application induite sur les H_i(X,Q) (ou les H^i(X,Q) ca revient au meme).
Ce theoreme etait important pour la stratégie de compréhension des conjectures de Weil qu'avait établi Grothendieck.
Mais il y avait bien sur d'autres resultats de nature plus geometrique, le theoreme de la section hyperplane de Lefshetz par exemple, ou le theoreme sur les classes (1,1) (de Lefshetz également), ou encore le theoreme de Lefshetz difficile (qui est un cousin du theoreme sur les sections hyperplanes). Bref on voulait une theorie cohomologique pour les variétés quelconques qui puisse nous permettre de disposer de ces theoremes sur un corps quelconques (et surtout un corps fini).
Il y avait d'autres contraintes, notamment on souhaitait disposer d'un bon theoreme de comparaison.
Bref toutes ces contraintes ont engendré la notion de cohomologie de Weil. Et la cohomologie des faisceaux n'est pas une cohomologie de Weil.
Une cohomologie de Weil pour les variétés algébriques est donné par la cohomologie étale. Et on savait (Grothendieck, Deligne et d'autres) que la simple existence d'une cohomologie de Weil pour les variétés algébriques sur les corps finis suffisait à prouver la quasi totalité des conjectures de Weil.
Il y a d'autres raisons a ne pas vouloir que le H^1 de C^* (ou de G_m en fait) soit nul. Par exemple si on veut une theorie des classes carracteristique, le fait que le H^1(C^*) soit non nul est assez crucial.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
