bjr,
je n'y connais rien mais je souhaitais vous aider...
L'espace projectif
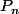
est le quotient de
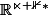
par la relation de colinéarité
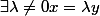
En particulier, on récupère la surjection de la sphère de dimension n
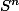
sur
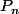
,qui passe au quotient, par l'antipodie
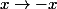
. Peut-on utiliser cette surjection canonique pour calculer ces groupes ? Il est probable qu'il faut utiliser des morphismes connus pour déterminer ces groupes.
Ou alors, au contraire, si ce sont des groupes décrivant une topologie "locale", utiliser alors un atlas et des cartes,les changements de cartes de l'espace projectif étant alors les homographies ?????
Cordialement,
PS: en regardant un
peuquelques remarques:
Les espaces projectifs de dimension paire ne sont pas orientables et
ceux de dimension impaire oui (sauf erreur). Ils sont tous connexes et compacts. Il se trouve que wiki donne un résultat sur les groupes de de Rham
dans ce cas là.
Si vous souhaitez faire les choses à la main, les formes p-linéaires
sont définies sur l'espace tangent en un point M0, de la sphère
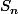
Par ailleurs, on a la différentielle de la surjection canonique
Ds en un point M0 de la sphère. En tant qu'application linéaire, elle transporte les vecteurs tangents de la sphère en M0, sur des vecteurs tangents de
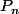
en
)
.
Pour une application p-linéaire

quelconque, sur l'espace tangent de
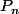
en
)
,
 \rightarrow \psi(Ds(u_1),Ds(u_2),..,Ds(u_p)))
est une application p_linéaire sur l'espace tangent de la sphère (on a composé par la différentielle).
On a donc différents objets:
1) espace vectoriel tangent
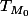
en un point sur la sphère,
isomorphe à
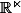
2) espace vectoriel des formes p-linéaires définies sur
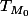
soit
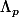
3) opérateur
d de différentiation extérieure qui envoie
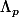
sur
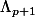
4) application linéaire Ds de la surjection canonique.
elle induit un morphisme de
)
sur
)
et doit avoir de bonnes propriétés avec l'opérateur
d.
5) enfin, la relation d'antipodie
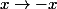
sur la sphère qui donne une relation entre espaces tangents aux antipodes.
Ensuite, dernier point, ces éléments d'algèbre multilinéaire en un point
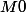
de la sphère sont paramétrés continuement quand le point M0 se "déplace" sur la sphère, et en particulier, que se passe-t-il quand le point M0 rejoint son point antipodal par un chemin

continu
sur la sphère. Ils disent que les espaces
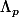
ont une structure de fibré ??
Mon conseil pour y voir clair:
a) regarder en un point M0 fixé de la sphère comment ça se passe, relativement à la surjection canonique de
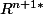
sur
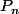
b) qu'est ce que ça devient aux antipodes ? changer le point

en le point
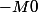
c) regarder ce qui se passe quand M0 varie continuement (d'abord localement sur un voisinage de
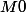
, puis globalement de
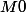
à
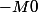
. On peut utiliser les coordonnées sphériques pour faire des calculs.)