Je vous remercie de votre aide, bonne soirée.
Carré et cube d'une somme à n éléments
14 messages
- Page 1 sur 1
carré et cube d'une somme à n éléments
Bonjour, je me trouve dans l'incapacité de prouver rigoureusement (je vois que ça marche) que 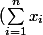^2=\sum_{i=1}^n x_i^2+2\sum_{i=1}^{n-1}{\sum_{j=i+1}^n x_ix_j}) ce qui me bloque pour la suite ...
ce qui me bloque pour la suite ...
Je vous remercie de votre aide, bonne soirée.
Je vous remercie de votre aide, bonne soirée.
Re: carré et cube d'une somme à n éléments
Bonjour,
Essayez par récurrence :
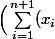\Big)^2=\Big(\big(\sum_{i=1}^n(x_i)\big)+x_{n+1}\Big)^2)
Et utilisez l'identité remarquable puis l'hypothèse de récurrence.
Essayez par récurrence :
Et utilisez l'identité remarquable puis l'hypothèse de récurrence.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: carré et cube d'une somme à n éléments
Polo a écrit:Bonjour, je me trouve dans l'incapacité de prouver rigoureusement (je vois que ça marche) quece qui me bloque pour la suite ...
Je vous remercie de votre aide, bonne soirée.
Salut,
Par récurrence, ça marche en remarquant que :
Puis en utilisant l'hypothèse de récurrence.
EDIT: hdci plus rapide.
Pseudo modifié : anciennement Trident2.
Re: carré et cube d'une somme à n éléments
Effectivement merci à vous deux, mais du coup comment je "fais un travail analogue" pour le cube ? compliqué pour moi tout ça ... Du coup c'est réellement par récurrence qu'il faut le démontrer ?
Re: carré et cube d'une somme à n éléments
Bonjour,
Sans récurrence, on peut faire :
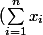^2=(\sum_{i=1}^{n} x_i )({\sum_{j=1}^n x_j})=\sum_{1\leq i,j \leq n} x_i x_j=\sum_{1\leq i,j \leq n, i=j} x_i x_j +\sum_{1\leq i,j \leq n, i \neq j} x_i x_j)
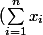^2=\sum_{1\leq i \leq n} x_i^2 +2\sum_{1\leq i<j \leq n} x_i x_j)
etc... il suffit d'arranger les indices pour retomber sur la formule (sur téléphone, les formules en latex c'est de l'acrobatie).
Sans récurrence, on peut faire :
etc... il suffit d'arranger les indices pour retomber sur la formule (sur téléphone, les formules en latex c'est de l'acrobatie).
Re: carré et cube d'une somme à n éléments
C'est ce qui se rapproche le plus de " la surface d'un carré de coté somme(xi)"
Re: carré et cube d'une somme à n éléments
D'accord merci beaucoup pour votre aide, donc pour le cube on peut faire de la même manière je suppose, je vais tester.
Re: carré et cube d'une somme à n éléments
Alors je trouve un résultat de cette façon faux mais proche du coup je me demande où j'ai pu me tromper si vous pouvez m'indiquer merci.
^3=\sum_{1\le i,j,k\le n} x_ix_jx_k=\sum_{1\le i,j,k\le n, i=j} x_ix_jx_k+\sum_{1\le i,j,k\le n, i\neq j} x_ix_jx_k)
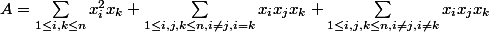
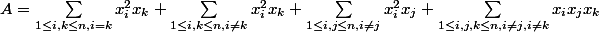
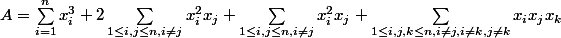
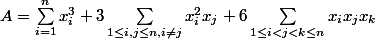
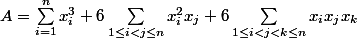
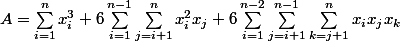
Or expérimentalement on observe que c'est un 3 devant la deuxième somme et je ne trouve pas mon erreur. Merci d'avoir lu mon message.
Or expérimentalement on observe que c'est un 3 devant la deuxième somme et je ne trouve pas mon erreur. Merci d'avoir lu mon message.
Re: carré et cube d'une somme à n éléments
Bonjour
Je vois au moins 2 erreurs la deuxième égalité de la première ligne (elle est bizarre) et puis l'avant dernière ligne qui est fausse en effet . Dans les termes en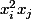 tu n'a pas de
tu n'a pas de 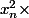 un
un  avec
avec 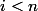
Or ton expression est symétrique au départ, elle l'est à l'arrivée.
Je vois au moins 2 erreurs la deuxième égalité de la première ligne (elle est bizarre) et puis l'avant dernière ligne qui est fausse en effet . Dans les termes en
Or ton expression est symétrique au départ, elle l'est à l'arrivée.
Re: carré et cube d'une somme à n éléments
De toute façon quand tu développes tu n'as que trois sortes de termes
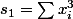
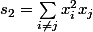
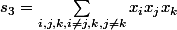
Donc l'expression à l'arrivée est de la forme
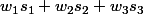
le tout est de compter pour avoir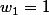 ,
, 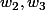
Donc l'expression à l'arrivée est de la forme
le tout est de compter pour avoir
Re: carré et cube d'une somme à n éléments
Salut,
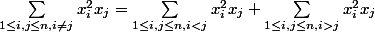
Comme i et j sont des variables "muettes " on peut remplacer dans la deuxième somme i et j (je pense que tu as bien compris cela mais ce que tu as oublié de faire c'est de modifier i et j a l'intèrieur de la somme)
Donc :
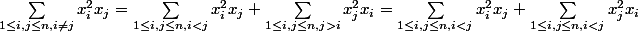
Donc c'est pas égal a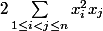 . Déjà cela résout le problème de symétrie qu'a souligné aviateur.
. Déjà cela résout le problème de symétrie qu'a souligné aviateur.
Comme i et j sont des variables "muettes " on peut remplacer dans la deuxième somme i et j (je pense que tu as bien compris cela mais ce que tu as oublié de faire c'est de modifier i et j a l'intèrieur de la somme)
Donc :
Donc c'est pas égal a
Re: carré et cube d'une somme à n éléments
Normalement avec le même raisonnement pour le carré d'une somme a n éléments tu devrais réussir sans passer par la récurrence.
Re: carré et cube d'une somme à n éléments
J'obtiens :
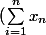^3=\sum_{i=1}^n x_i^3+3\sum_{i=1}^{n-1}\sum_{j=i+1}^n (x_i^2x_j+x_j^2x_i)+6\sum_{i=1}^{n-2}\sum_{j=i+1}^{n-1}\sum_{k=j+1}^n x_ix_jx_k)
ce qui me semble être la bonne réponse merci pour votre aide.
ce qui me semble être la bonne réponse merci pour votre aide.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
