Calculer une intégrale par récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 17 Juil 2014, 20:47
par Mikihisa » 17 Juil 2014, 20:47
Bonjour !
Exercice demande de calculer par récurrence l'intégrale suivante :
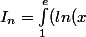)^n dx/)
En faisant une intégration par partie (avec u= log^(n-1) et v'=log) j'obtiens la relation suivante :
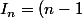.(I_{n-2}-I_{n-1})
Vous avez des idée sur comment calculer In avec ça ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 17 Juil 2014, 21:03
par Sa Majesté » 17 Juil 2014, 21:03
Salut !
Si tu intègres par partie avec u=ln^n et v'=1, tu tombes sur une relation de récurrence plus simple
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 17 Juil 2014, 21:06
par Mikihisa » 17 Juil 2014, 21:06
Ah ! J'avais essayer dans ma tête et j'ai eu l'impression de tomber sur un truc stéril, Atta je le fait sur papier ^^
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 17 Juil 2014, 21:21
par Mikihisa » 17 Juil 2014, 21:21
En effet je trouve In = e-n.In-1
D'instinct j'airais donc
^k}{(n-k)!} +\frac{1}{e} -1))
mais jvais essayer le montrer par récurrence ça doit pas être dur.
Merci
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 17 Juil 2014, 21:28
par Mikihisa » 17 Juil 2014, 21:28
Oups j'me suis tromper il fait s'arrêter a n=1 m'enfin j'serais me débrouiller *^
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 18 Juil 2014, 00:21
par deltab » 18 Juil 2014, 00:21
Bonsoir
Mikihisa a écrit:Oups j'me suis tromper il fait s'arrêter a n=1 m'enfin j'serais me débrouiller *^
La relation

donne la forme
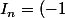^n(\alpha_ne-\beta_n))
.
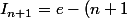I_n=(-1)^{n+1}((n+1)\alpha_ne+e-(n+1)\beta_n)
.
Les suites
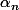
et
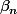
vérifient alors
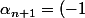^{n+1}(n+1)\alpha_n e +e)
et
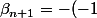^{n+1}(n+1)\beta_n)
Reste à expliciter
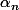
et
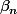
.
PS: Le titre du post était-il la question?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 18 Juil 2014, 11:23
par adrien69 » 18 Juil 2014, 11:23
Mikihisa a écrit:En effet je trouve In = e-n.In-1
D'instinct j'airais donc
^k}{(n-k)!} +\frac{1}{e} -1))
mais jvais essayer le montrer par récurrence ça doit pas être dur.
Merci
D'instinct ^^
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 18 Juil 2014, 17:54
par Mikihisa » 18 Juil 2014, 17:54
Bawi en développant deux ou trois fois a la main on vois tout de suite que
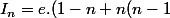+...+n!) - (-1)^{n}.n!I_1)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 18 Juil 2014, 22:07
par Mikihisa » 18 Juil 2014, 22:07
Monologue je sais ... En fait j'ai galerer car j'avais mal anticiper les borne de la sommes, il fallais l'arrêter à n-2, la reccurence se fait bien et l'égalité est vrai pour n=2
^k.n!}{(n-k)!} -(-1)^n.n!(\frac{1}{e} -1))
Je pensais pas galerer autant ....
Next :p
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 20 Juil 2014, 03:18
par deltab » 20 Juil 2014, 03:18
Bonjour.
Je corrige les erreurs de mon 1er post
La relation

donne la forme
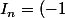^n(\alpha_n e-\beta_n))
.
On aura donc
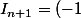^{n+1}(\alpha_{n+1}e-\beta_{n+1}))
Mais
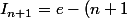I_n=(-1)^{n+1}((n+1)\alpha_ne+e-(n+1)\beta_n)
En comparant les deux écritures de
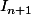
, on déduit que:
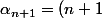\alpha_n+1)
et
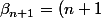\beta_n)
d'où

-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 20 Juil 2014, 05:28
par deltab » 20 Juil 2014, 05:28
Bonjour.
Je corrige les erreurs de mon 1er post
La relation

donne la forme
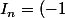^n(\alpha_n e-\beta_n))
.
On aura donc
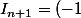^{n+1}(\alpha_{n+1}e-\beta_{n+1}))
Mais
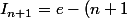I_n=e+(-1)^{n+1}((n+1)\alpha_n e-(n+1)\beta_n)
En comparant les deux écritures de
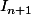
, on déduit que:
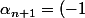^{n+1}+(n+1)\alpha_n)
et
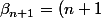\beta_n)
d'où

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités