Calculer une intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
SuperPoule
- Membre Naturel
- Messages: 50
- Enregistré le: 03 Juin 2021, 09:09
-
 par SuperPoule » 07 Avr 2024, 14:24
par SuperPoule » 07 Avr 2024, 14:24
Bonjour,
En surfant sur youtube, j'ai vu cette intégrale (et malheureusement je n'arrive pas à retrouver la vidéo) :
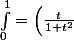^n\;dt)
J'ai essayé plusieurs petits trucs (IPP, changement de variable), mais je n'arrive à rien et du coup j'en viens à me demander si j'ai bien lu...
Auriez-vous une idée ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Avr 2024, 18:18
par Ben314 » 07 Avr 2024, 18:18
Salut,
Sans trop réfléchir, si pour

tu pose
^b}\,dt)
alors tu as une première relation triviale
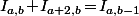
et une intégration par partie (
^{-b})
) va t'en donner une deuxième.
Et je pense qu'avec les deux, tu calcule ce que tu veut (par contre, je sais pas si les sommes obtenues se simplifient bien).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
SuperPoule
- Membre Naturel
- Messages: 50
- Enregistré le: 03 Juin 2021, 09:09
-
 par SuperPoule » 08 Avr 2024, 13:15
par SuperPoule » 08 Avr 2024, 13:15
Bonjour Ben314,
OK, merci pour ton aide, je vais voir ce que cela donne.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Avr 2024, 16:38
par Ben314 » 08 Avr 2024, 16:38
En posant
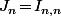
(qui est ce que tu cherche), après quelques pérégrination, je trouve que
\ ;\ J_2\!=\!\dfrac{\pi-2}{8})
puis, pour
(n\!-\!2)2^n}+\dfrac{n-3}{4(n-2)}J_{n-2})
qui permet éventuellement d'écrire
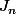
sous forme d'une somme (finie), mais, à priori, ça ne se simplifie pas franchement. . .
On pourrait aussi utiliser le développement en série entière de
^{-n})
pour obtenir une expression du résultat sous forme de série.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 09 Avr 2024, 18:20
par catamat » 09 Avr 2024, 18:20
Bonjour
Ce qui est amusant c'est qu'après les deux premiers termes non rationnels, on a
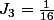
car dans la formule de récurrence le deuxième terme s'annule.
On peut d'ailleurs le calculer directement par IPP :
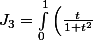^3\;dt)
On pose
=t^2)
et
=\frac{t}{(1+t^2)^3})
on a
=2t)
et
=\frac{1}{-4}\times\frac{1}{(1+t^2)^2})
donc
^2}\right]_0^1+\frac{1}{2}\int_0^1 \frac{t}{(1+t^2)^2}\;dt=\frac{-1}{16}+\frac{1}{2}\left[\frac{1}{-2}\times\frac{1}{1+t^2}\right]_0^1=\frac{-1}{16}-\frac{1}{8}+\frac{1}{4}=\frac{1}{16})
Finalement tous les

, avec k entier non nul, sont des nombres rationnels d'après la formule de Ben314.
Par contre, les termes de rang pair, supérieur à 2, vont contenir


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Avr 2024, 18:25
par Ben314 » 09 Avr 2024, 18:25
Oui, c'est un peu étonnant que seul
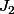
"contiennet" du logarithme. Et je suis pas allé chercher plus loin pour voir s'il y avait une raison simple à ce fait : j'y suis allé tel le bourrin en écrivant les relations de récurrence donnant
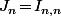
et

en fonction de

et

puis j'ai tripatouillé pour virer les

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
