Calcul de la surface d'un ballon de rugby

[Vander]

Bonsoir s'il vous plait quelqu'un pourrais m'aider a calculer la surface d'un ballon de rugby obtenue par rotation(d'angle v) autour de l'axe (Oz) de l'ellipse de plan(yOz). Je vous remercie d'avance !

[Dlzlogic]

Bonjour,
Je ne sais pas si c'est un exercice, en tout cas, je suis sûr que c'est très difficile.
Par contre, il existe des méthodes qui donnent une très bonne approximation, tout à fait compatible avec la surface de cuir nécessaire.
Donc, il faudrait plus de détails.

[Ericovitchi]

l'aire d'un ellipsoïde :
si a la demi longueur du grand axe et b celle du petit axe et e l’excentricité donné par

Si l'ellipsoïde est aplati l'aire est donnée par

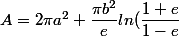Si l'ellipsoïde est allongé (ce qui est de bon aloi pour un ballon de rugby) alors


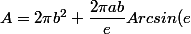Pour la démonstration voir ici

[fatal_error]

Hi Vander,

ton ellipse s'écrit (à peu près)
ay^2+bz^2=1.
Si tu écris z en fonction de y, tu as qqch du genre
z=sqrt( (1-ay^2)/b ) (pour z positif)

du coup, tu as une fonction f(z) qui va générer ta surface.
T'as juste à dessiner des couronnes f(z),f(z+dz) à calculer l'aire de toutes ces couronnes.

Ce qui te donne (pour z>0) qqch du genre
integrale 2pi f(z) * dz*f'(z)
où 2pi f(z) représente le périmètre d'une couronne élémentaire, et f'(z)dz son épaisseur

Je peux me tromper..mais ca à l'air pas trop mal

[Vander]

Bonjour, a vous tous je tenais tout d'abord a vous remercier pour vos reponses. Voila j'ai un peu cherche et je suis confu. L'aire d'un ballon de rugby obtenue par rotation (d'angle v) autour de l'axe(Oz) de l'ellipse de plan(yOz) est t-elle la meme que celle de l'ellipse d'equation y^/b^ + z^/c^=1. Car lorsque je calcul l'aire de cette elipse je trouve A=pi*ab .
Demonstration : changement de variable y=brcos;) et z=crsin;). J=(bcos;) -crsin;), bsin;) crcos;)) donc detJ=bcr, dydz=bcrdrd;) et ;)={(r,;)) € R*R, 0<=r<=1 et 0<=;)<=2pi } A=integrale double f(y,z)dydz=ab integrale double*rdrd;)=pi*ab. J'ai vraiment besoin de savoir si l'aire de cette ellipse est la meme que celle du ballon de rugby. Merci encore a vous !