Calcul d'une surface sphérique
14 messages
- Page 1 sur 1
Calcul d'une surface sphérique
Bonjour à tous,
Je cherche à déterminer la surface sphérique définie par un ensemble (nuage) de points, dont les coordonnées tridimensionnelles sont exprimées dans le référentiel associé à la sphère (origine au centre).
Je pense que la 1ère étape doit consister à déterminer la forme convexe qui circonscrit tous les points.
Merci.
Je cherche à déterminer la surface sphérique définie par un ensemble (nuage) de points, dont les coordonnées tridimensionnelles sont exprimées dans le référentiel associé à la sphère (origine au centre).
Je pense que la 1ère étape doit consister à déterminer la forme convexe qui circonscrit tous les points.
Merci.
Bonjour,
cette théorie
harmoniques sphériques
permet de décrire le relief terrestre. ça semble marcher comme des séries de Fourier, mais en 3D.
Cette théorie semble ardue mais devrait te permettre d'obtenir une fonction
et une équation (sans doute avec des séries) décrivant au mieux la surface cherchée.
sinon, idée perso:
a) déterminer l'enveloppe convexe
b) un convexe est l'intersersection d'hyperplan
c) un (hyper)plan affine est déterminé par un point A
par lequel il passe et par un vecteur normal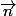
d) ton convexe va donc te donner une famille finie
de couples constitué d'un point et d'un vecteur normal) , A et
, A et 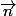 étant fonctions des coordonnées (x,y,z)
étant fonctions des coordonnées (x,y,z)
du lieu de l'espace euclidien où ils se trouvent.
e)
si f(x,y,z)=0 est l'équation cherchée de la surface,
le gradient de f coincide avec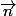
il ne te reste plus qu'à trouver, par une méthode numérique,
une fonction "spatiale" dont le gradient est connu en n points.
Ecrit autrement, les plans tangents à la surface seont ceux de l'enveloppe convexe.
est-ce que les B-splines existent en dimension 3 ? sans doute que oui.
cette théorie
harmoniques sphériques
permet de décrire le relief terrestre. ça semble marcher comme des séries de Fourier, mais en 3D.
Cette théorie semble ardue mais devrait te permettre d'obtenir une fonction
et une équation (sans doute avec des séries) décrivant au mieux la surface cherchée.
sinon, idée perso:
a) déterminer l'enveloppe convexe
b) un convexe est l'intersersection d'hyperplan
c) un (hyper)plan affine est déterminé par un point A
par lequel il passe et par un vecteur normal
d) ton convexe va donc te donner une famille finie
de couples constitué d'un point et d'un vecteur normal
du lieu de l'espace euclidien où ils se trouvent.
e)
si f(x,y,z)=0 est l'équation cherchée de la surface,
le gradient de f coincide avec
il ne te reste plus qu'à trouver, par une méthode numérique,
une fonction "spatiale" dont le gradient est connu en n points.
Ecrit autrement, les plans tangents à la surface seont ceux de l'enveloppe convexe.
est-ce que les B-splines existent en dimension 3 ? sans doute que oui.
re,
voilà quelque chose de simple, je ne sais si ça correspond aux besoins:
on a les points M_i en coordonnées cartésiennes)
on passe en coordonnées sphériques
M_i en coordonnées sphériques,r_i sin(\theta_i)cos(\phi_i),r_i sin(\theta_i)sin(\phi_i)))
on cherche la sphère des "moindres carrés" (l'expression est de moi)
qui rend minimale la somme
^2)
on développe, on calcule la fonction dérivée de ce trinôme de la variable r
et on trouve la sphère , centrée en O, de rayon moyen :hum:
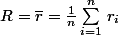
résultat affligeant de banalité
ps: maintenant, si tu souhaite une surface douce (smooth) qui passe par les points extremaux du nuage, là, il y a sûrement plus de travail...
attendre que Nuage rentre de vacances... :zen:
voilà quelque chose de simple, je ne sais si ça correspond aux besoins:
on a les points M_i en coordonnées cartésiennes
on passe en coordonnées sphériques
M_i en coordonnées sphériques
on cherche la sphère des "moindres carrés" (l'expression est de moi)
qui rend minimale la somme
on développe, on calcule la fonction dérivée de ce trinôme de la variable r
et on trouve la sphère , centrée en O, de rayon moyen :hum:
résultat affligeant de banalité
ps: maintenant, si tu souhaite une surface douce (smooth) qui passe par les points extremaux du nuage, là, il y a sûrement plus de travail...
attendre que Nuage rentre de vacances... :zen:
re,
içi
peux tu indiquer le problème ?
le nuage est il grosso modo inscrit dans une sphère ? dans un ellipsoïde ?
il a un vingtaine de points ou plusieurs millions de points ? etc ?
quel est le but ?
içi
peux tu indiquer le problème ?
le nuage est il grosso modo inscrit dans une sphère ? dans un ellipsoïde ?
il a un vingtaine de points ou plusieurs millions de points ? etc ?
quel est le but ?
Bonjour et merci pour ces réponses,
L'objectif final est de calculer un angle solide (implémentation logicielle).
Tous les points sont par définition sur la sphère.
Après réflexion, j'envisageais la démarche suivante:
- détermination du polygone circonscrit;
- facétisation (triangles) du polygone;
- somme des angles solides des facettes (http://fr.wikipedia.org/wiki/Angle_solide).
Cordialement,
L'objectif final est de calculer un angle solide (implémentation logicielle).
Tous les points sont par définition sur la sphère.
Après réflexion, j'envisageais la démarche suivante:
- détermination du polygone circonscrit;
- facétisation (triangles) du polygone;
- somme des angles solides des facettes (http://fr.wikipedia.org/wiki/Angle_solide).
Cordialement,
ah, on ne s'est pas du tout compris. Je croyais qu'il fallait déterminer
l'enveloppe d'un nuage de points de l'espace euclien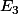
En fait, il faut calculer un angle solide,,ie, mesurer l'aire de l'enveloppe d'un ensemble fini de points, tous situés sur la sphère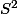 (de rayon 1).
(de rayon 1).
On dispose de la mesure de Lebesgue sur la sphère (??).
Déja, pour n'importe quelle mesure
= \mu(A)+\mu(A)- \mu(A \cap B))
cf
ps: il n'y a pas de groupe des angles (solides) , ni modulo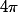
ni autrement, comme pour le cercle.
l'enveloppe d'un nuage de points de l'espace euclien
En fait, il faut calculer un angle solide,,ie, mesurer l'aire de l'enveloppe d'un ensemble fini de points, tous situés sur la sphère
On dispose de la mesure de Lebesgue sur la sphère (??).
Déja, pour n'importe quelle mesure
cf
ps: il n'y a pas de groupe des angles (solides) , ni modulo
ni autrement, comme pour le cercle.
re,
le sujet dépasse mes compétences...
quelques idées à tout hasard:
1) est-ce que l'on peut adapter la formule de green-riemann
à la sphère (tenir compte de la courbure), ce qui ramènerait
un calcul d'aire à une intégrale d'une forme différentielle
sur le bord,ie, sur les arcs de cercles de l'enveloppe convexe ?
içi
2°) Est-ce que l'on peut tenter la méthode de Monte-Carlo de calcul d'aire
(on bombarde la sphère avec des points aléatoires: la proportion de points
situés à l'intérieur du domaine donne l'aire)
quelques indications de trigo sphérique:
i) sur la sphère de rayon 1, la longueur d'un côté d'un triangle
est la mesure en radian de l'angle au centre de la sphère qui intercepte l'arc
ii) les angles des triangles, en un sommet A, sont les angles des vecteurs tangents aux côtés (vecteurs situés dans le plan tangent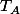 ), les côtés étant vus comme des arcs de cercles paramétrés.
), les côtés étant vus comme des arcs de cercles paramétrés.
iii) il y a une formule donnant l'aire d'un triangle sphérique
iv) il y a une notion très pratique: celle de triangle polaire A'B'C'
du triangle sphérique ABC. Les deux triangles échangent leurs angles et leurs côtés. Les côtés de l'un sont les angles de l'autre et réciproquement.
le sujet dépasse mes compétences...
quelques idées à tout hasard:
1) est-ce que l'on peut adapter la formule de green-riemann
à la sphère (tenir compte de la courbure), ce qui ramènerait
un calcul d'aire à une intégrale d'une forme différentielle
sur le bord,ie, sur les arcs de cercles de l'enveloppe convexe ?
içi
2°) Est-ce que l'on peut tenter la méthode de Monte-Carlo de calcul d'aire
(on bombarde la sphère avec des points aléatoires: la proportion de points
situés à l'intérieur du domaine donne l'aire)
quelques indications de trigo sphérique:
i) sur la sphère de rayon 1, la longueur d'un côté d'un triangle
est la mesure en radian de l'angle au centre de la sphère qui intercepte l'arc
ii) les angles des triangles, en un sommet A, sont les angles des vecteurs tangents aux côtés (vecteurs situés dans le plan tangent
iii) il y a une formule donnant l'aire d'un triangle sphérique
iv) il y a une notion très pratique: celle de triangle polaire A'B'C'
du triangle sphérique ABC. Les deux triangles échangent leurs angles et leurs côtés. Les côtés de l'un sont les angles de l'autre et réciproquement.
Surface nuage de points
Bonjour,
Je reprends exactement la question posée dans le tout premier message de ce sujet : j'aurais besoin de calculer la surface d'un ensemble de points dont j'ai les coordonnées sphériques (r,theta,phi).
Quelqu'un saurait-il comme je peux calculer la surface du volume concerné? sachant que c'est un ellipsoïde.
Existe-t-il sous Matlab un algorithme permettant de calculer l'intégrale double d'une fonction discrète à deux variables (ici r(theta,phi)) en coordonnées sphériques? Je n'en ai pas trouvé de toute faite.
Avez-vous connaissance d'un algorithme performant pour ce genre de problème?
Merci d'avance pour votre aide.
Cordialement
Je reprends exactement la question posée dans le tout premier message de ce sujet : j'aurais besoin de calculer la surface d'un ensemble de points dont j'ai les coordonnées sphériques (r,theta,phi).
Quelqu'un saurait-il comme je peux calculer la surface du volume concerné? sachant que c'est un ellipsoïde.
Existe-t-il sous Matlab un algorithme permettant de calculer l'intégrale double d'une fonction discrète à deux variables (ici r(theta,phi)) en coordonnées sphériques? Je n'en ai pas trouvé de toute faite.
Avez-vous connaissance d'un algorithme performant pour ce genre de problème?
Merci d'avance pour votre aide.
Cordialement
mathelot a écrit:re,
içi
peux tu indiquer le problème ?
le nuage est il grosso modo inscrit dans une sphère ? dans un ellipsoïde ?
il a un vingtaine de points ou plusieurs millions de points ? etc ?
quel est le but ?
salut,
tu t'inspires de mathelot avec les moindres carrés: tu as ton eq dellipsoide : x^2/a^2+y^2/b^2+z^2/c^2=1 (me semble til)
tu fais une minimisation des ecarts quadratiques (pratiques tu as une fonction toute faite pour ca, leasqr (pour octave, je présume que pour matlab aussi).
Ca te détermine tes paramètres a,b, et c.
Il ne te reste plus qu'à calculer la surface de l'ellipsoide. Ca doit se faire à la mano, j'en sais rien.
Par ordi, tu peux par exemple, créer plein de facettes en créant plein de point (par exemple deux ellipses à z et z+dz).
Tu peux sinon apparemment t'en sortir avec un truc que j'ai pas trop regardé ici
Quelqu'un saurait-il comme je peux calculer la surface du volume concerné? sachant que c'est un ellipsoïde.
tu t'inspires de mathelot avec les moindres carrés: tu as ton eq dellipsoide : x^2/a^2+y^2/b^2+z^2/c^2=1 (me semble til)
tu fais une minimisation des ecarts quadratiques (pratiques tu as une fonction toute faite pour ca, leasqr (pour octave, je présume que pour matlab aussi).
Ca te détermine tes paramètres a,b, et c.
Il ne te reste plus qu'à calculer la surface de l'ellipsoide. Ca doit se faire à la mano, j'en sais rien.
Par ordi, tu peux par exemple, créer plein de facettes en créant plein de point (par exemple deux ellipses à z et z+dz).
Tu peux sinon apparemment t'en sortir avec un truc que j'ai pas trop regardé ici
la vie est une fête 
Bonjour,
Tour d'abord, par surface vous entendez "forme", "fonction", ou au contraire "superficie", "aire".
Je crois qu'il y a eu ambiguïté dans le début de ce fil.
Le réponse de Fatal_erreur concerne les 2 hypothèses.
Ce que je voulais ajouter est que le calcul de la longueur d'un arc d'ellipse est difficile, et je crois même impossible, par contre on obtient une très bonne approximation de l'ellipse avec une parabole. La longueur d'un arc de parabole se calcule avec une très bonne précision, c'est à dire aussi précisément qu'on veut.
Mais pour calculer l'aire d'un ellipsoïde, sauf le diviser en facettes, j'ai pas d'idée.
Tour d'abord, par surface vous entendez "forme", "fonction", ou au contraire "superficie", "aire".
Je crois qu'il y a eu ambiguïté dans le début de ce fil.
Le réponse de Fatal_erreur concerne les 2 hypothèses.
Ce que je voulais ajouter est que le calcul de la longueur d'un arc d'ellipse est difficile, et je crois même impossible, par contre on obtient une très bonne approximation de l'ellipse avec une parabole. La longueur d'un arc de parabole se calcule avec une très bonne précision, c'est à dire aussi précisément qu'on veut.
Mais pour calculer l'aire d'un ellipsoïde, sauf le diviser en facettes, j'ai pas d'idée.
Dlzlogic a écrit:Mais pour calculer l'aire d'un ellipsoïde, sauf le diviser en facettes, j'ai pas d'idée.
je sais pas si en paramétrisant ça marche. Pour une sphère on paramétrise avec les coordonnées sphériques puis on intègre la normale suivant les deux angles qui varient. Par contre là, le module r varie donc ...
Cryptocatron-11 a écrit:je sais pas si en paramétrisant ça marche. Pour une sphère on paramétrise avec les coordonnées sphériques puis on intègre la normale suivant les deux angles qui varient. Par contre là, le module r varie donc ...
Bonjour,
On peut diviser la surface d'une sphère en triangles. Il y a des triangles qui dont 1/6 d'hexagone, et des triangles qui sont 1/5 de pentagone (cf ballon de foot-ball)
Chacun de ces triangles est ensuite divisé en 4. On arrête la subdivision quand on en a assez. :we:
Enfin, il n'y a plus qu'une multiplication et une addition à faire.
On peut raisonner en math pures, mais comme je crois que le calcul de la longueur d'une ellipse est impossible, il me parait probable qu'il en est de même pour l'aire.
En fait, on ne sait pas dans quel contexte la question est posée, on n'a eu de retour, ni de l'un, ne de l'autre questionneur.
Bonsoir,
Tout d'abord, merci à tous pour vos réponses.
Je vais vous donner de plus amples précisions sur ce dont je dispose, ce que je veux calculer et dans quel contexte je fais ça. Ensuite, je vous expliquerai ce que j'ai fait, peut-être que certains connaisseurs pourront me donner de nouvelles idées.
Alors, je fais de la physique en fait, de la mécanique des fluides diphasique plus précisément. J'ai un code de calcul Navier-Stokes en 3D qui calcule sur maillage cartésien la déformation d'une bulle au cours du temps. Je récupère de ce code l'intersection de l'interface de la bulle avec mon maillage. J'ai donc un ensemble de points exprimés en coordonnées cartésiennes.
Mon objectif : calculer l'aire de cette interface (définie par un ensemble de points) de quelque manière que ce soit (en intégrant manuellement l'élement de surface (mais comment le discrétiser au mieux?), en utilisant des algorithmes déjà existants (lesquels?)...).
Je précise que la forme de ma bulle est globalement un ellipsoïde, mais ce n'est pas un ellipsoïde parfait (je regarde notamment la forme que prend ma bulle lorsqu'un tourbillon arrive dessus, elle est donc complexe).
Ce que j'ai fait pour le moment, et qui reprend certaines des idées qui ont été formulées dans vos messages précédents :
- j'ai calculé les coordonnées sphériques de l'ensemble de mes points
- j'ai utilisé une fonction Matlab d'interpolation sur la sphère, de manière à interpoler des points sur un maillage sphérique uniforme (plus facile par la suite de réaliser des intégrations en ayant dtheta = cste et dphi = cste).
- j'ai paramétrisé l'interface comme une sphère, mais avec "r" variable (dépendant de theta et phi) puis j'ai retrouvé l'expression classique de l'élément de surface correspondant. Cet élement de surface dépend de la dérivée de r par rapport à theta et phi.
- pour l'instant, j'ai intégré l'élément de surface, en le discrétisant de manière simple (différences finies d'ordre 1).
ça marche, quand je calcule la surface d'un sphéroïde aplati et que je compare avec la solution analytique, j'obtiens une erreur qui converge à l'ordre 1 en fonction du nombre de points d'interpolation que je choisis.
J'aurais voulu savoir si vous aviez déjà traité un problème similaire (calculer l'aire de la surface définie par un ensemble de points discrets, sur la sphère), et si donc vous connaissiez des discrétisations plus malignes de l'élément de surface ou des fonctions Matlab (ou sur tout autre logiciel) toutes faites pour calculer des surfaces d'ellipsoïde (je n'ai pas trouvé pour le moment).
Merci en tous cas d'avoir pris la peine de lire mon problème et éventuellement d'y répondre.
Cordialement
Tout d'abord, merci à tous pour vos réponses.
Je vais vous donner de plus amples précisions sur ce dont je dispose, ce que je veux calculer et dans quel contexte je fais ça. Ensuite, je vous expliquerai ce que j'ai fait, peut-être que certains connaisseurs pourront me donner de nouvelles idées.
Alors, je fais de la physique en fait, de la mécanique des fluides diphasique plus précisément. J'ai un code de calcul Navier-Stokes en 3D qui calcule sur maillage cartésien la déformation d'une bulle au cours du temps. Je récupère de ce code l'intersection de l'interface de la bulle avec mon maillage. J'ai donc un ensemble de points exprimés en coordonnées cartésiennes.
Mon objectif : calculer l'aire de cette interface (définie par un ensemble de points) de quelque manière que ce soit (en intégrant manuellement l'élement de surface (mais comment le discrétiser au mieux?), en utilisant des algorithmes déjà existants (lesquels?)...).
Je précise que la forme de ma bulle est globalement un ellipsoïde, mais ce n'est pas un ellipsoïde parfait (je regarde notamment la forme que prend ma bulle lorsqu'un tourbillon arrive dessus, elle est donc complexe).
Ce que j'ai fait pour le moment, et qui reprend certaines des idées qui ont été formulées dans vos messages précédents :
- j'ai calculé les coordonnées sphériques de l'ensemble de mes points
- j'ai utilisé une fonction Matlab d'interpolation sur la sphère, de manière à interpoler des points sur un maillage sphérique uniforme (plus facile par la suite de réaliser des intégrations en ayant dtheta = cste et dphi = cste).
- j'ai paramétrisé l'interface comme une sphère, mais avec "r" variable (dépendant de theta et phi) puis j'ai retrouvé l'expression classique de l'élément de surface correspondant. Cet élement de surface dépend de la dérivée de r par rapport à theta et phi.
- pour l'instant, j'ai intégré l'élément de surface, en le discrétisant de manière simple (différences finies d'ordre 1).
ça marche, quand je calcule la surface d'un sphéroïde aplati et que je compare avec la solution analytique, j'obtiens une erreur qui converge à l'ordre 1 en fonction du nombre de points d'interpolation que je choisis.
J'aurais voulu savoir si vous aviez déjà traité un problème similaire (calculer l'aire de la surface définie par un ensemble de points discrets, sur la sphère), et si donc vous connaissiez des discrétisations plus malignes de l'élément de surface ou des fonctions Matlab (ou sur tout autre logiciel) toutes faites pour calculer des surfaces d'ellipsoïde (je n'ai pas trouvé pour le moment).
Merci en tous cas d'avoir pris la peine de lire mon problème et éventuellement d'y répondre.
Cordialement
Dlzlogic a écrit:Bonjour,
On peut diviser la surface d'une sphère en triangles. Il y a des triangles qui dont 1/6 d'hexagone, et des triangles qui sont 1/5 de pentagone (cf ballon de foot-ball)
Chacun de ces triangles est ensuite divisé en 4. On arrête la subdivision quand on en a assez. :we:
Enfin, il n'y a plus qu'une multiplication et une addition à faire.
On peut raisonner en math pures, mais comme je crois que le calcul de la longueur d'une ellipse est impossible, il me parait probable qu'il en est de même pour l'aire.
En fait, on ne sait pas dans quel contexte la question est posée, on n'a eu de retour, ni de l'un, ne de l'autre questionneur.
Bonjour,
Voilà ce que j'ai compris.
On a une bulle dont on veut mesurer l'aire de l'interface avec le milieu extérieur.
Cette bulle est connue par un ensemble de points en coordonnées cartésiennes (XYZ).
Ces points définissent une sphère "moyenne", ou plutôt, il existe une sphère telle que la somme des carrés des distances des points à la sphère soit minimum.
L'aire de cette sphère est l'aire minimum possible de l'interface entre la bulle et le milieu extérieur.
Chaque point observé peut être considéré comme une "anomalie locale". Etant donné la distance de ce point à la sphère, cette "anomalie" peut être chiffrée.
Cette méthode basée sur une "somme de corrections indépendante" me semble beaucoup plus précise qu'une modélisation théorique d'un faux ellipsoïde.
PS Mille pardons, je n'avais pas regardé les dates des messages.
Voilà ce que j'ai compris.
On a une bulle dont on veut mesurer l'aire de l'interface avec le milieu extérieur.
Cette bulle est connue par un ensemble de points en coordonnées cartésiennes (XYZ).
Ces points définissent une sphère "moyenne", ou plutôt, il existe une sphère telle que la somme des carrés des distances des points à la sphère soit minimum.
L'aire de cette sphère est l'aire minimum possible de l'interface entre la bulle et le milieu extérieur.
Chaque point observé peut être considéré comme une "anomalie locale". Etant donné la distance de ce point à la sphère, cette "anomalie" peut être chiffrée.
Cette méthode basée sur une "somme de corrections indépendante" me semble beaucoup plus précise qu'une modélisation théorique d'un faux ellipsoïde.
PS Mille pardons, je n'avais pas regardé les dates des messages.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
