Calcul de somme de series

[Adoniram]

Voila, quelqu'un pourrait il m'indiquer le process a suivre pour calculer ce genre de somme de series :

Somme de k=0 a infini de An.X^n avec An= 2A(n-1) +1 et A0 = 4
Bon je sais me dépatouiller de la suite arithmético-géométrique et exprimer An en fonction de n. C'est pour le reste que je n'ai pas de méthodologie :/
Merci d'avance :)

[Anonyme]

Adoniram
Peux tu confirmer que le nième "terme" de ta série entière est avec

ps)
c'est une suite géométrique de raison 2 donc la suite diverge donc la série ....

[Anonyme]

@Adoniram

Soit la suite définie par avec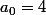

Cette suite est une suite dite "arithmético-géométrique"
et si cette suite converge vers un nombre alors on a :
c'est à dire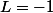

Posons la suite définie par c'est à dire

Cette suite est une suite géométrique de raison 2 car avec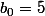

à toi de calculer en fonction de n le terme
puis d'essayer d'utiliser des critères de convergence / de calculs de séries à termes positifs

[Adoniram]

Bonjour, j'arrive a me debrouiller de la suite
définie par avec j'ai = non, mon problème est pour transformer cette somme en une fonction f(x) ne dépendant que de x...

[Pythales]

Bonjour, j'arrive a me debrouiller de la suite
définie par avec j'ai = non, mon problème est pour transformer cette somme en une fonction f(x) ne dépendant que de x...

En fait soit
ce qui revient
1) A déterminer le rayon de convergence
2) A calculer la somme de 2 séries géométriques

[Adoniram]

non, en fait mon problème semble plus simple, tout simplement je cherche la démarche pour transformer cette somme en fonction f(x)
D’après ce que j'entrevois, je dois chercher le rayon de convergence de mes deux séries et définir leur somme... Est ce bien cela ?

[Anonyme]

@doniram]non

OK je crois que j'ai compris : tu recherches l'expression de la fonction telle que
avec qui appartient au disque de convergence de cette série entière

Merci de confirmer (ou de me dire que j'ai rien compris)
A+

[Adoniram]

Je trouve pour ma première suite un rayon de convergence de 1/2 et pour la suite un rayon de convergence de 1 . Je dois revoir mes calculs ou bien je peux continuer ?

[Adoniram]

@doniram]non

OK je crois que j'ai compris : tu recherches l'expression de la fonction telle que
avec qui appartient au disque de convergence de cette série entière

Merci de confirmer (ou de me dire que j'ai rien compris)
A+

OUIIII c'est ca avec les caractéristiques de telles que je les donne plus haut... Mon soucis majeur est que je ne connais pas la marche a suivre pour résoudre ce problème.
Merci pour le coup de mains, et pour le temps que vous prenez

[Anonyme]

@Adoniram

La méthode est (et cela semble logique)
1) calculer le rayon de convergence
2) calculer l'expression de la limite en


Relis le message de Pythales qui a répondu à ta question en 1 seul et unique message.
Tu ne l'as peut être pas lu ou compris à cause de moi (qui parasite cette discussion)
Si c'est le cas je suis désolé
A+

[Adoniram]

En fait je l'ai compris partiellement : mes ryons de convergences des deux series sont ils bons ? 1/2 et 1 ? Dans le cas positif, que dois je faire ensuite de ces deux rayons et de ces deux series ?

[Anonyme]

@Adoniram

A mon avis avec ce raisonnement
tu ne peux pas conclure que le rayon de convergence de la série est 1/2

Car avant de pouvoir "couper" en 2 LA somme d'une série : il faut être sûr de la convergence de cette série


donc d'après moi tu ne peux écrire que
que si tu connais déjà le rayon de convergence de cette série

et pour calculer le rayon de convergence de cette série tu peux utiliser des théorèmes comme Cauchy ou d'Alembert...

[Adoniram]

aaaah s'eut été trop facile... et du coup pas si simple le rayon de convergence...

[Anonyme]

@Adoniram

1) Connais tu comment on calcule le rayon de convergence d'une série entière ?

2) La suite est "positive" et on connait l'expression du terme en fonction de
Connais tu les théorèmes de d'Alembert ou de Cauchy ?

[Adoniram]

mmmm je m'en sors pas du rayon de convergence tout d'un bloc... j'essaye de resoudre mais ca me conduit a rien que je sache reduire

[Anonyme]

@Adoniram
Je ne comprends pas où est le problème : calcule la limite de quand tend vers


ps)
C'est important d'expliciter que

[Adoniram]

mmmm je m'en sors pas du rayon de convergence tout d'un bloc... j'essaye de resoudre mais ca me conduit a rien que je sache reduire

Voyons voir, puis-je ecrire : c'est a dire 1 quand n tend vers l'infini ?

[Anonyme]

Voyons voir, puis-je ecrire : c'est a dire 1 quand n tend vers l'infini ?

je ne comprends pas ce que tu as écrit

La limite de quand tend vers est très simple à calculer....


limite de limite de

[Adoniram]

Et avec ce rayon de convergence, il me faut en faire quoi a present ?

[Anonyme]

Et avec ce rayon de convergence, il me faut en faire quoi a present ?

Tu peux enfin (ouf !!) utiliser le 2) du message de Pythales