Calcul racine carrée; racine nieme nombre complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 25 Oct 2020, 20:07
par novicemaths » 25 Oct 2020, 20:07
Bonsoir
1)Calculer les racines carrées du nombre complexe
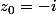
sous forme algébrique et exponentielle.
J'ai trouvé sous forme algébrique
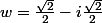
et
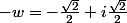
Sous forme exponentielle:
D'abord,

et
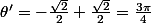
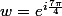
et
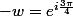
2)Calculer les racine troisième du nombre complexe
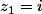
.

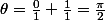
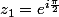
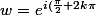})
avec k=3
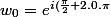} = e^{i\frac{\pi}{2}})
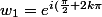} = e^{i(\frac{\pi}{2}+2.1.\pi)} = e^{i(\frac{\pi}{2}+2\pi)} e^{i(\frac{\pi}{2}+\frac{4\pi}{2})} = e^{i\frac{5\pi}{2}})
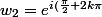} = e^{i(\frac{\pi}{2}+2.2.\pi)} = e^{i(\frac{\pi}{2}+ 4\pi)} = e^{i(\frac{\pi}{2}+ \frac{8\pi}{2})} =e^{i\frac{9\pi}{2}})
Pourriez- vous me dire si les calculs sont correctes?
A bientôt
-
Black Jack
 par Black Jack » 26 Oct 2020, 14:39
par Black Jack » 26 Oct 2020, 14:39
2)
Ce n'est pas correct ...
Réfléchis sur ce qui suit :
w³ = i
w³ = e^(i.(Pi/2 + 2k.Pi))
w = e^(i.(Pi/6 + 2k.Pi/3))
a) k = 0
w0 = e^(i.(Pi/6) = cos(Pi/6) + i.sin(Pi/6) = (V3)/2 + (1/2).i
b) k = 1
w1 = e^(i.(Pi/6 + 2Pi/3) = e^(i.5Pi/6) = cos(5Pi/6) + i.sin(5Pi/6) = -(V3)/2 + (1/2).i
c) k = 2
w2 = e^(i.(Pi/6 + 4Pi/3) = e^(i.3Pi/2) = cos(3Pi/2) + i.sin(3Pi/2) = -i
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 26 Oct 2020, 14:57
par novicemaths » 26 Oct 2020, 14:57
Bonjour
Pourquoi avez-vous mis
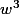
?
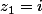
n'est pas à la puissance au cube.
A bientôt
-
Black Jack
 par Black Jack » 26 Oct 2020, 16:34
par Black Jack » 26 Oct 2020, 16:34
novicemaths a écrit:Bonjour
Pourquoi avez-vous mis
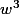
?
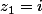
n'est pas à la puissance au cube.
A bientôt
"Calculer
les racines troisièmes du nombre complexe z1 = i ."
Il faut donc trouver les nombres complexes w tel que w³ = z1
Donc trouver les nombres complexes w tel que w³ = i
OK ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 26 Oct 2020, 16:43
par novicemaths » 26 Oct 2020, 16:43
Je vais refaire tout les calculs

A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 26 Oct 2020, 21:08
par Pisigma » 26 Oct 2020, 21:08
Bonsoir,
dans ton cas particulier, tu pourrais résoudre l'exercice en utilisant uniquement la factorisation
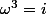
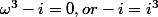
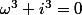
de la forme
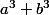
(\omega^2-\omega\,i-1)=0)
\left[(\omega-\dfrac{i}{2})^2-(\dfrac{\sqrt{3}}{2})^2\right]=0)
entre les [ ] on a une expression de la forme

d'où les 3 racines
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 27 Oct 2020, 18:40
par novicemaths » 27 Oct 2020, 18:40
Bonsoir
Voici mes nouveaux calculs.

On peut s'simplifier le dernier
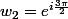
Est-ce que c'est correcte?
A bientôt

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 27 Oct 2020, 19:14
par Sa Majesté » 27 Oct 2020, 19:14
novicemaths a écrit:
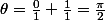
J'ai du mal avec ce genre d'écriture.
Que veux-tu dire ?
Pour moi
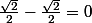
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 27 Oct 2020, 19:41
par novicemaths » 27 Oct 2020, 19:41
Sa Majesté

c'est l'argument.
J'ai du faire une erreur.
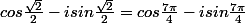
A bientôt
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 27 Oct 2020, 22:48
par ijkl » 27 Oct 2020, 22:48
novicemaths a écrit: 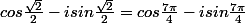
Bah c'est faux
mais de toute façon je ne vois vraiment pas d'où vous sortez des racines carrées (ou cubiques) dans ce sujet
quand on doit écrire une racine n ième d'un nombre complexe, les racine carrées on les laisse au placard
on prend l'argument principal (dans l'intervalle
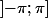
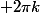
avec k dans Z et on divise par n le tout et pour le module on prend ce module et on le met à la puissance 1/n et tout argument de ce résultat sera celui-là
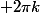
j'ai jamais vu l'écriture d'une racine carrée ou cubique ou racine n ième dans un truc comme ça mais bon ....
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 29 Oct 2020, 17:18
par novicemaths » 29 Oct 2020, 17:18
Bonjour
Voici le détail du calcul de racine carré de -i

Ci-dessous le détaille du calcul de la racine troisième de i.

J'espère que la c'est correcte.
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 29 Oct 2020, 19:14
par Pisigma » 29 Oct 2020, 19:14
1) c'est quoi le - devant

2) si
=-\dfrac{\sqrt{2}}{2})
et
=\dfrac{\sqrt{2}}{2},~~~~ \theta=\dfrac{3\pi}{4})
remarque la façon de faire est assez lourde, perso je préfère ce qui suit
Deux nombres complexes(non nuls) sont égaux ssi ils ont même module et même argument modulo

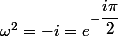
égalité des modules
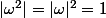
donc
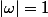
égalité des arguments modulo

=2 arg(\omega)=-\dfrac{\pi}{2}+2 k\pi)
avec
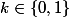
=-\dfrac{\pi}{4}+k\pi)
ce qui donne 2 solutions
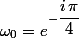
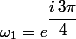
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 10 Nov 2020, 21:02
par novicemaths » 10 Nov 2020, 21:02
Bonsoir
On me demande détaillé les calcules.
Le

, c'est pour différencier la racine négative et positive.
Concernant le calcul de la racine troisième de nombre complexe, je me suis aidé de cette vidéo (ci-dessous).
https://youtu.be/wTHyuA1UOGMDans la dernière question on demande de déterminer la racine sixième de nombre complexe en m'aidant des résultat des deux questions précédente.
Je ne vois pas quelle méthode utiliser, j'ai essayé en utilisant les règles de calcul des exponentielles.
Pourriez-vous me guider ?
A bientôt
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 07:49
par Pisigma » 11 Nov 2020, 07:49
Concernant le calcul de la racine troisième de nombre complexe, je me suis aidé de cette vidéo (ci-dessous).
Dans la dernière question on demande de déterminer la racine sixième de nombre complexe en m'aidant des résultat des deux questions précédente.
de quels nombres complexes?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 11 Nov 2020, 18:44
par novicemaths » 11 Nov 2020, 18:44
Bonsoir
1)
On a trouvait les racines carrées de
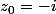
sous forme exponentielle.
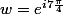
et
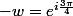
2)
Et on a trouvait les racines troisième de
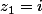
sous forme exponentielle.
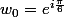
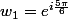
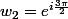
3)
Je cherche la racine sixième de
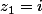
avec les résultat 1) et 2).
Je ne vois pas quelle méthode à employer.
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
?
n'est pas à la puissance au cube.