Nombre complexes - racine nième

[joquetino]

Bonsoir à tous,

J'aimerais savoir s'il y a un moyen de trouver les racines cubiques de 52+47i ?
Je cherche donc les réels a et b, tels que (a+ib)^3 = 52 + 47i

En développant (a+ib)^3, j'arrive à un calcul un peu compliqué. Ai-je raté quelque chose ?

Je vous remercie pour votre aide,

[GaBuZoMeu]

Le carré du module de ton nombre est . Bon début !
Au fait, .

[lyceen95]

Développer , ce n'est pas si compliqué. Au niveau supérieur, ça ne doit pas poser de problème.
Ensuite, c'est plus compliqué, on a des équations du 3ème degré.
Je me suis dit que les valeurs 52 et 47 ne venaient pas de n'importe où, et que cette équation avait probablement une racine a+ib avec a et b entiers. Et effectivement, en cherchant avec des entiers 'simples', on trouve rapidement une racine.
Les 2 autres racines sont alors faciles à trouver.

Montre où tu en es, et des gens t'aideront à continuer, ou à corriger tes erreurs.

[jsvdb]

Salut !
Pour appuyer les dires de lyceen95, 47 est un nombre premier, ce qui va encore plus vite dans les calculs de recherche d'entiers solution.

[GaBuZoMeu]

En quoi le fait que 47 soit premier aide-t-il ? Tu penses à un calcul modulaire ?

Si l'on cherche des solutions dans les entiers de Gauss (de la forme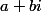 avec entiers), la considération du module est primordiale : le carré du module doit être le cube d'un entier qui se décompose comme somme de deux carrés.

[joquetino]

Merci à tous. J'ai pu m'en sortir avec votre aide.

[GaBuZoMeu]

Qu'as-tu fait, si ce n'est pas indiscret ?

[joquetino]

Voici comme j'ai procédé. A vrai dire, j'avais déjà la réponse avant de vous poser la question, mais j'avais du mal à présenter la façon d'arriver au résultat.

Soit u un complexe
on cherche u^3=(52+47i) (ou 52-47i)

or module de U^3 = (module U)^3 = module (52-47i)=(Racine 17)^3
Je pose u =a+ib (a et b entiers relatifs)

donc (racine(a^2+b^2))^3=(racine(17))^3
j'en déduis que a^2 + b^2 = 17

Or 1^2+4^2=17

Les solutions possibles sont donc :
(1+4i) ; (-1+4i) ; (-1-4i);(1-4i)
(4+i)) ; (-4+i) ; (-4-i) ; (4-i)

En testant certaines de ces valeurs, j'en déduis que (4+i)^3 = 52+47i

Cela vous semble valable comme réponse ?

[lyceen95]

Est-ce que l'exercice disait qu'on cherchait spécifiquement un nombre a+ib avec a et b ENTIERS ?

- Tu dis Or 1²+4²=17 donc les solutions possibles sont ... ... et tu donnes une liste de 8 complexes.
Il faut que tu sois plus précis. Il faut dire : Or 1²+4²=17 et c'est la seule façon d'écrire 17 comme somme de 2 carrés entiers.

[joquetino]

Tout à fait, on cherche bien des entiers pour a et b.
Merci pour ta remarque en tout cas.

[GaBuZoMeu]

Merci, c'est bien le module qui joue le rôle de premier plan ici.

[jsvdb]

En quoi le fait que 47 soit premier aide-t-il ? Tu penses à un calcul modulaire ?

Du tout, je plussoyais simplement la remarque de lyceen95.


On doit avoir donc soit soit le contraire.

Si 47 n'avais pas été premier, c'eût été un peu plus long (et on n'en serait pas là, comme dirait Ray Ventura )

Et j'avoue n'avoir pas pensé au module de prime abord. Ce qui est peut-être un tort si la puissance n'avait pas été 3 mais une bien plus élevée.