Calcul de limite avec calcul integral
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 11 Mar 2015, 20:04
par Rik95 » 11 Mar 2015, 20:04
Bonsoir,
Quelqu'un pourrai m'aider a trouver ces limites en utilisant le calcul intégral svp, je galère un peu a trouver l'astuce ...
lim quand n tend vers + l'infini de : n/n²+1 + n/n²+2² + n/n²+3² + ... + n/n²+n²
et aussi de : ln(n/n+1)^1/n + ln(n/n+2)^1/n + ln(n/n+3)^1/n + ... +ln(n/n+n)^1/n
Merci d'avance :)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 11 Mar 2015, 20:12
par Joker62 » 11 Mar 2015, 20:12
Hello,
On cherche :
^2})
et après on pense aux sommes de Riemann.
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 12 Mar 2015, 22:54
par Rik95 » 12 Mar 2015, 22:54
Merci pour ta réponse, donc pour les sommes de Riemann dans ce cas la est ce que je peu poser ceci ? :
f(x) = 1/x
a = 1, b = 2 car b -a = 1 ( en prenons 1/n = b-a /n )
parcontre je n'ai pas d'idée pour le moment en ce qui concerne le k²/n² qui me gene ...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Mar 2015, 07:14
par Joker62 » 13 Mar 2015, 07:14
Hello,
Si f est intégrable au sens de Riemann sur [a;b] alors :
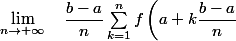 \quad = \quad \int_a^b \quad f(x)\text{dx})
Ici pour la première a = 0 ; b = 1 ; et f(x) = 1/(1+x^2)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 13 Mar 2015, 15:22
par Rik95 » 13 Mar 2015, 15:22
Je vois ^^, en appliquant la formule de riemann ainsi j'ai trouvé que la lim est egal a pi/4, est ce que c'est correct ?
J'ai essayer d'utiliser le meme principe pour calculer la 2eme et j'ai trouvé 2 -2 ln(2) en ayant pris f(x) = ln(1/1+x) avec b =1 et a = 0
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Mar 2015, 17:21
par Joker62 » 13 Mar 2015, 17:21
Hello,
Je ne sais pas il manque trop de parenthèses pour que je prenne parti :)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 13 Mar 2015, 17:32
par Rik95 » 13 Mar 2015, 17:32
La voici ^^

-
mathelot
 par mathelot » 13 Mar 2015, 19:15
par mathelot » 13 Mar 2015, 19:15
Avec cette somme de Riemann, on trouve comme limite, quand n tend vers l'infini:
1-2ln(2)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 14 Mar 2015, 14:41
par Rik95 » 14 Mar 2015, 14:41
Merci pour ta reponse, mais je ne trouve pas le meme resultat, en refaisant le calcul je trouve -2ln(2) +1 ... je ne vois pas ou est mon erreur :/
-
mathelot
 par mathelot » 14 Mar 2015, 16:31
par mathelot » 14 Mar 2015, 16:31
Rik95 a écrit:Merci pour ta reponse, mais je ne trouve pas le meme resultat, en refaisant le calcul je trouve -2ln(2) +1 ... je ne vois pas ou est mon erreur :/
au temps pour moi. :hum: tous les log de la somme sont négatifs.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités

