Calcul Integrale

[Pisigma]

personnellement je partirais de



soit en divisant haut et bas par (avec

[george154]

En quoi poser u=tan(t) va m'aider pour trouver une primitive ?
Je vois pas ce qui pourrait ressembler à (1+u^2)/(1-u^2)

[george154]

Je pourrais avoir la solution avec les explications pour je comprennes ?

[Pisigma]

à remplacer dans l'équation de départ; attention (ne pas oublier de changer les bornes de l'intégrale!!)

[george154]

J'en étais à intégrale de 0 à pi/6 de I+J = intégrale de 0 à pi/6 de 1/cos(2t) en sachant que 1/cos(2t) = (1+u^2)/1+u^2) avec u=tan(t). Jusque là je suis d'accord mais je ne comprends pas ce que je dois faire après. Comment je suis censé me ramener à une primitive connue pour pouvoir enfin calculer cette intégrale.

[Pisigma]

I+J devient


soit

[george154]

Je peux avoir un rédaction complète dans l'ordre parce que je suis vraiment perdu… Je m'excuse j'essaye vraiment de comprendre mais j'ai beaucoup de mal. Comment on passe de ce que j'ai à votre première intégrale ? En quoi la dernière intégrale va-t-elle me permettre de conclure ?

[Pisigma]

pour terminer le calcul le quotient final, doit être décomposé en fractions simples

[george154]

Si on prend la calculatrice pour vérifier, l'intégrale I+J donnée au départ n'est pas égale à celle que vous me donnez dans votre précédent message. Il n'y a pas une erreur quelque part ?

[Pisigma]

tu t'es trompé on trouve exactement la même chose quand on calcule en t ou en u; à savoir

[george154]

Ta dernière intégrale c'est pas : intégrale de 0 à (racine de 3) / 3 de (1+tan^2(t)) / (1-tan^2(t) dt ?

[Pisigma]

non pas du tout ; relis le coefficient de l'intégrale; il y a des simplifications, il ne reste que 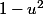au dénominateur

tu n'as plus de t

[george154]

u n'est pas égal à tan(t) ?

[Pisigma]

si mais tu as changé de variable et tes bornes d'intégration aussi

[george154]

Est ce que tu peux me faire une explication depuis le début détaillé pour que je puisses en discuter avec mon prof demain ? Parce que vraiment j'ai pas tout bien compris.

[Pisigma]

il suffit de lister chronologiquement mes posts

de 14h06; (18h06); 18h32;19h11;19h37 et 19h55 et tu auras l'ensemble du raisonnement

[george154]

Du coup pour le tout dernier calcul décomposé en fractions simples, j'en fais quoi exactement ? Cela correspond à quel primitive ?

[Pisigma]

quand tu as trouvé A et B ça revient à intégrer 2 fractions qui donneront "du ln"

[george154]

A et B sont des réelles ?

[Pisigma]

oui

tu n'as jamais décomposé en fractions simples?

si ce n'est pas indiscret, quelle formation suis-tu?