Calcul d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gloui
- Messages: 1
- Enregistré le: 12 Déc 2019, 11:56
-
par gloui » 12 Déc 2019, 12:02
Bonjour,
Je dois résoudre l'intégrale suivante, sauf que j'ai un niveau assez basique sur ce sujet.
 dx = - \mu f(\mu))
De ce que j'ai compris on peut décomposer l'intégrale
 dx + \frac{d}{d \mu} \int_{c}^{\infty} xf(x) dx)
Je suppose que l'intégrale de droite, étant donnée, qu'elle ne dépends pas de mu, en la dérivant on obtient zéro. Puis pour celle de gauche je ne sais pas trop.
Merci d'avance pour votre aide
-
mathelot
par mathelot » 12 Déc 2019, 12:31
gloui a écrit:Bonjour,
Je dois résoudre l'intégrale suivante, sauf que j'ai un niveau assez basique sur ce sujet.
De ce que j'ai compris on peut décomposer l'intégrale
Je suppose que l'intégrale de droite, étant donnée, qu'elle ne dépends pas de mu, en la dérivant on obtient zéro. Puis pour celle de gauche je ne sais pas trop.
Merci d'avance pour votre aide
Supposons f continue.
)
est continue sur
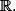
Elle admet une primitive F.
F est donc dérivable et F'(x)=xf(x)
 dx =\frac{d}{d \mu} \left(F(c)-F(\mu)\right)=-\mu f(\mu))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
