Calcul intégrale

[Aud0908]

Bonjour,

Je dois calculer l'intégrale suivante :

où F est une distribution uniforme avec distribué sur .

Du coup, pour simplifier l'écriture de l'intégrale et trouver une primitive plus facilement, puis-je écrire que cette même intégrale est équivalente à ?

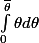
Comme ici .

Merci par avance.

[Sake]

Salut,

J'imagine que par distribution uniforme tu es en train de parler de densité de probabilité d'une loi uniforme sur [0,1], et dans cette affaire est une variable aléatoire qui suit la-dite loi uniforme ?
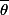
Je comprends pas le qu'il faudrait que tu précises.

[Aud0908]

Bonjour,

Oui c'est exactement ça !

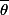
Le est une valeur de quelconque qui appartient à l'intervalle.

[pascal16]

souvent on note f la fonction de densité et F celle de répartition (qui vaut 1 sur [1;+oo[)
si tu essaies d'intégrer "xdx", c'est de la fonction de répartition dont tu calcules l'intégrale

[Aud0908]

Bonjour,
Je n'ai pas compris votre réponse.
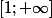
Ici la fonction de répartition F n'est pas définie sur mais sur .
Comme l'on sait que pour une loi uniforme où et sont les bornes de l'intervalle (0 et 1 ici), alors dans mon exemple .
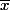
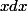
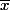
Du coup ce que je me demande c'est si je fois intégrer entre 0 et est-ce que cela est équivalent à intégrer entre 0 et ? (puisque que comme je le dis ci-dessus dans mon cas .)

Merci de nouveau.

[pascal16]

Perso, j'ai plutôt appris que F était définie sur R entier :
pour x<0, F(x)=0
pour x>1, F(x)=1
pour 0 ≤ x ≤ 1, F(x)=x
ainsi,on peut faire tous les calculs qu'on veut même avec plusieurs va.