Calcul integral
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 09 Mai 2015, 11:35
par Sake » 09 Mai 2015, 11:35
Bonjour,
Une idée de la manière dont on calcule une primitive de
^e)
là où elle existe ?
Merci,

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Mai 2015, 12:07
par Ben314 » 09 Mai 2015, 12:07
Salut,
Si je te dit que ça fait
\Gamma(e+1,-\ln(t))\)
où

est la
fonction Gamma incomplète, ça te va ?
(dixit Wolfram...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 09 Mai 2015, 12:35
par Sake » 09 Mai 2015, 12:35
hmmm non pas vraiment ^^ C'est le raisonnement qui m'intéresse.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Mai 2015, 13:39
par Ben314 » 09 Mai 2015, 13:39
Ben du raisonnement, y'en a quasiment pas....
En posant
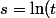)
on a
)^e\,dt=\int_?^{\ln(x)}s^e\exp(s)\,ds)
et c'est quasiment la définition de la fonction "gamma incomplète" (c.f. wiki) avec a=e+1
Enfin, si on a "inventé" cette fonction "gamma incomplète", j'aurai un soupons tendance à penser que c'est parce que, à part cas particulier (a entier où à la limite rationnel par exemple) on ne sait pas exprimer cette intégrale avec les "fonctions élémentaires".
Et comme là, e+1 c'est pas trop entier (ni rationnel), je pense pas qu'on puisse écrire grand chose d'autre.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 09 Mai 2015, 15:49
par Sake » 09 Mai 2015, 15:49
Ben314 a écrit:Ben du raisonnement, y'en a quasiment pas....
En posant
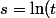)
on a
)^e\,dt=\int_?^{\ln(x)}s^e\exp(s)\,ds)
et c'est quasiment la définition de la fonction "gamma incomplète" (c.f. wiki) avec a=e+1
Enfin, si on a "inventé" cette fonction "gamma incomplète", j'aurai un soupons tendance à penser que c'est parce que, à part cas particulier (a entier où à la limite rationnel par exemple) on ne sait pas exprimer cette intégrale avec les "fonctions élémentaires".
Et comme là, e+1 c'est pas trop entier (ni rationnel), je pense pas qu'on puisse écrire grand chose d'autre.
Oui, c'est ce que j'ai fait en partant de 0 jusqu'à x (parce qu'en 0,
)^e = 0)
), mais j'ai voulu développer en suite en faisant une IPP et c'est clairement ce qu'il ne fallait pas faire. Je n'ai pas vu la fonction gamma incomplète à ce niveau et j'ai cherché à l'obtenir avec l'IPP (ce qui se fait par la suite mais c'est clairement plus compliqué).
Merci pour ton aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
où
est la fonction Gamma incomplète, ça te va ?
on a