Calcul de la k-iémé dérivé

[matmuay]

Bonjour
Avez vous une idée de comment calculer la
k-iéme dérivée par rapport à z de
f(x)= ch(n*(h+z))/ch(nz)

Merci

[busard_des_roseaux]

Bonjour
Avez vous une idée de comment calculer la
k-iéme dérivée par rapport à z de
f(x)= ch(n*(h+z))/ch(nz)

Merci

Bj,





f est donc une fonction affine de la quantité th(nx)

il reste à évaluer la dérivée k-ième de th()

1er aspect
th() admet un développement en série de Taylor .
On obtient ainsi le résultat demandé sous forme d'une série
en dérivant termes à termes

2ème aspect
th() vérifie une équation différentielle


ce qui suggère d'écrire



soit



on obtient donc , par une récurrence immédiate, la dérivée
k-ième de l'application réciproque:



il se trouve qu'il y a une formule (franchement imbuvable)
qui relie la dérivée n-ième d'une fonction bijective aux
dérivées k_ième () de sa fonction réciproque.

[busard_des_roseaux]

re,

avec des notations hardies (Hardy ?):

on pose:


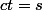
les fonctions dérivées donnent:

coefficient du binôme

écrivons 2n dérivations de l'égalité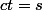 avec les
formules de (dérivation d'un produit de) Leibnitz:


obtenir une expression pour la dérivée (2n)ième de la fonction th()
revient donc à inverser la matrice:



Cette matrice a un déterminant non nul

l'inversion de cette matrice ne devrait pas poser problème
aux lecteurs :doh:

comme et , doit-on écrire la matrice comme la somme d'une diagonale
et d'une nilpotente ? en tous cas, ça a l'air intéressant à inverser.

[busard_des_roseaux]

re,

quelqu'un sait inverser cette grande matrice ?

elle est triangulaire inférieure, c et s représentent ch(x)
et sh(x), on peut calculer la somme des coeff. de chaque ligne.