Calcul domination de suites

[aviateur]

Ah oui tu a oublié le 4 peut être?

Sinon est-ce que tu comprends (là où tu nages) qu'il faut seulement mettre un O(1/n^2) car il n'y a que cela à comprendre!!!!

[mehdi-128]

J'ai les termes :




Or la suite (1/n) est bornée donc :



De même :

On obtient :



D'après le cours :



Et : car la suite (1/n^2) est bornée

Finalement on obtient :

[aviateur]

Oui c'est ça. Bon ce qu'il faut retenir maintenant (et je crois qu'on te l'a déjà dit au dessus)
toute cette partie avec un peu d'habitude on ne la détaille pas.
C'est à dire que dès que tu as un O(1/n^2) tout le reste qui te donnera un grand O(1/n^2) il est déjà comptabiliser dans le premier que tu as écrit. Autrement ce calcul en écriture il doit être très court

[LB2]

@Ben

Mon livre n'explique rien à part la définition et met des exemples comme si on devait comprendre par la magie du saint esprit comment ça marche ça m'énerve les auteurs comme ça

Si je fais le calcul comme vous m'avez dit :



Et là je nage complet.

Mais non c'est bon, regarde tous tes termes parasites sont du O(1/n^2).

Il faut que tu comprennes que tous les termes de la forme A/n^2, B/n^3, C/n^4 etc. sont aussi du O(1/n^2)

EDIT : Je n'avais pas vu le message d'aviateur, mais c'est exactement ça

[mehdi-128]

Oui c'est ça. Bon ce qu'il faut retenir maintenant (et je crois qu'on te l'a déjà dit au dessus)
toute cette partie avec un peu d'habitude on ne la détaille pas.
C'est à dire que dès que tu as un O(1/n^2) tout le reste qui te donnera un grand O(1/n^2) il est déjà comptabiliser dans le premier que tu as écrit. Autrement ce calcul en écriture il doit être très court

D'accord par contre une dernière chose j'ai pas compris pourquoi on laisse pas :

au lieu de ça change quoi ?

[Pseuda]

D'accord par contre une dernière chose j'ai pas compris pourquoi on laisse pas :
au lieu de ça change quoi ?

Parce qu'on veut du (un développement avec cette précision), on n'a que faire du , et qui peut le plus peut le moins car : .
(mais : ).

[Pseuda]

En tout cas, ce fil m'a éclairée sur la notation O qui m'échappait encore un peu.

[aviateur]

On peut même se familiariser avec cela mais

[mehdi-128]

D'accord par contre une dernière chose j'ai pas compris pourquoi on laisse pas :
au lieu de ça change quoi ?

Parce qu'on veut du (un développement avec cette précision), on n'a que faire du , et qui peut le plus peut le moins car : .
(mais : ).

Ah d'accord merci oui fait faire attention la relation de domination n'est pas réflexive !
Elle est juste transitive.

[aviateur]

si elle est réflexive mais pas symétrique

[mehdi-128]

si elle est réflexive mais pas symétrique

Oui vous avez raison j'ai fait une gaffe

[mehdi-128]

Maintenant je suis en train d'étudier les petits o et j'ai un doute :

Je veux montrer un résultat trivial : quelque soit la suite

Je sais qu'il suffit de montrer que la limite de : est nulle si ne s’annule pas à partir d'un certain rang mais comment je suis sûr que la suite ne pas pas s'annuler à partir d'un certain rang ?

[aviateur]

ce n'est pas la bonne définition.

ssi il existe une suite 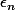qui tend vers 0 tel que



ici puisque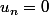 , pour tout n alors 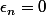pour tout n (même si un peut s'annuler

[mehdi-128]

Merci aviateur du coup la définition avec les limites s'applique que si on est sûr que la suite (vn) ne s'annulera pas ?

[aviateur]

Oui la définition que je te donne est générale mais dans la pratique on utilise ce que tu dis sauf cas particulier où on revient cette définition qui englobe tous les cas

[mehdi-128]

Une autre petite question sur les petit o.

Après calcul et l'utilisation d'un théorème : pour tendant vers 0 et f une fonction dérivable sur un intervalle contenant 0.

On trouve :

L'auteur dit : "dernière relation pas très parlante" pourquoi

Ensuite on trouve :



Pourquoi la deuxième relation serait plus parlante que la première ?

[aviateur]

Uniquement parce qu'elle te donne plus de renseignements.


Par exemple si on te demande limite de (cos(u_n)-1)/u_n^2
avec la première tu ne epux rien dire avec la deuxième tu trouves -1/2.

[mehdi-128]

Ah d'accord merci