Domination asymptotique

[Maxim]

Bonjour à tous, j'essaye de comprendre un texte mathématique en rapport avec mon TIPE et je butte sur quelque chose qui a l'air facile :

On veut montrer que m(n) domine n.log(n) et on a trouvé m(n) >= log n! - log n.

Maintenant je suppose qu'il faut utiliser Stirling : log n! = n.log n + O(n)
donc m(n) >= n.log n + O(n)

Pourquoi ceci implique-t-il m(n) = GrandTheta (n.log(n)) ? :hein:

Merci pour votre aide

[ToToR_2000]

Bonjour,
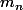
d'abord, si alors on dit que domine et pas l'inverse me semble-t-il...
De plus on dit "grand O" et pas grand theta.
Pour ta question, c'est bon signe que tu aies des difficultés à le prouver puisque c'est faux: prends

[Maks]

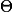
Attention, la notation existe, et est différente de , ce me semble.

[Maxim]

En fait je voulais dire GrandOmega et pas GrandTheta...
je veux bien montrer m(n)=GrandOmega(n.log n), soit m(n) domine n.log n
(ce qui est il me semble équivalent à n.log n est dominée par m(n))...

[ToToR_2000]

et bien justement c'est faux, d'où mon contre-exemple

[Maxim]

J'ai l'impression aussi que c'est faux, mais m(n) = n²log n n'est pas un contre-exemple (on a alors bien n.log n=O(m_n), doit m_n domine n.log n), me semble-t-il...