voila c'est peut etre bete mais je bloque sur le calcul suivant:
on doit déterminer z tel que:
3e^2z + 1 + 2i = i
Merci d'avance
Calcul de complexe
8 messages
- Page 1 sur 1
Re: Calcul de complexe
Salut
C'est exp(2)×z ou bien exp(2z) ?
C'est exp(2)×z ou bien exp(2z) ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Calcul de complexe
Sharkk a écrit:voila c'est peut etre bete mais je bloque sur le calcul suivant:
on doit déterminer z tel que:
3e^2z + 1 + 2i = i
Merci d'avance
Cela équivaut à:
Exp(2z) = (-i-1)/3
Connais-tu le logarithme complexe? La détermination principale Log?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Calcul de complexe
Voila, je bloque la justement!!
Non nous n'avons pas appris , ou du moins pas encore !
, ou du moins pas encore !
Non nous n'avons pas appris
 , ou du moins pas encore !
, ou du moins pas encore !Re: Calcul de complexe
Sharkk a écrit:Voila, je bloque la justement!!
Non nous n'avons pas appris, ou du moins pas encore !
Tu peux essayer de poser z = x + iy
Puis essaye d'identifier parties réelles et parties imaginaires des deux membres:
exp(2x)cos(2y) = -1/3
exp(2x)sin(2y)= - 1/3
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Calcul de complexe
Plus explicitement

Donc
y est un argument de donc y est égal à
donc y est égal à 
En clair l'ensemble des solutions sont les
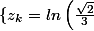 + i(\frac{5\pi}{4} + 2k\pi), k \in \mathbb{Z}\})
Donc
y est un argument de
En clair l'ensemble des solutions sont les
Re: Calcul de complexe
lionel52 a écrit:Plus explicitement
Donc
y est un argument dedonc y est égal à
En clair l'ensemble des solutions sont les
Sans oublier le facteur 2 qui traine vu qu'on cherche 2z.
Et puis... donner des solutions toutes faites n'est pas vraiment dans l'esprit du forum...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
