Calcul approché

[Martin4545]

Bonjour,
Je suis en train d'etudier un livre sur la relativité et une méthode de calcul approché me donnes des problémes....

On a :

x=2\frac{L}{c}[\frac{1}{1-\frac{v^{2}}{c^{2}}}-\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}]

Et on a c>>v

Donc :

x\approx 2\frac{L}{c}[1+\frac{v^2}{c^2}-(1+\frac{v^2}{2c^2}) ]

Voilà et je ne comprends pas vraiment comment on atteint ce résultat

Ps: je suis nouveau

[LB2]

Bonjour,






Pour passer d'une formule à l'autre, on utilise ce qu'on appelle les approximations affines ou développements limités au premier ordre. C'est valable ici uniquement car est très petit devant 1.

On peut donner un sens plus précis mathématiquement à ce que signifie cette approximation, mais les physiciens se contentent souvent de ce "approximativement égal à " (sans avoir besoin d'évaluer précisément la valeur de la différence et donc la qualité de l'approximation).

On utilise, pour x "proche de 0" ou "petit devant 1", les formules suivantes :

valables pour tout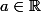 , et utilisées ici pour et

[Martin4545]

Bonsoir,
Merci de cette réponse rapide cela m'aide beaucoup.
Dans mon livre ils utilisent une technique étrange dont j'aimerais connaître le nom voici un example :

Pour x=(y+z) ^n
1. On multiplie et on divise par y^n

y^n\frac{(y+z) ^n}{y^n}=y^n[1+(\frac{z}{y})]^n
2. On développe l'expression entre crochets selon la formule du binôme et on neglige tous les termes sauf le premier

Voilà et je ne comprends pas comment appliquer cette technique à mon cas...

[LB2]

Cela revient au cas précédent que j'ai exposé
en posant x = z/y, lorsque z/y est très petit devant 1, c'est à dire z très petit devant y.
et avec un exposant entier a = n.

On peut en effet développer la parenthèse selon la formule du binôme de Newton (qui est une généralisation à des exposants entiers quelconque de l'identité remarquable

et tous les termes sauf le premier pourront être négligés devant z/y car comporteront respectivement (z/y)^2, (z/y)^3, ..., (z/y)^n.
Dans la terminologie des développements limités, on dit que les termes en z/y sont "d'ordre un" ou "du premier ordre" et tous les termes en (z/y)^2, (z/y)^3, etc. sont d'ordre supérieur.