Bonjour,
Je dois, en utilisant le binôme de Newton, donner l'expression de A^n en fonction de n en sachant que la matrice A (3*3) est :
(2 1 0
0 2 0
0 0 3)
que la matrice B vaut :
( 0 1 0
0 0 0
0 0 0) et B^n=O3^(n-1)B en gros la matrice nulle
j'ai tout d'abord admis qu'on pouvais écrire A sous la forme aI3+bB=( a 0 0/ 0 a 0/ 0 0 a)+b(0 1 0/ 0 0 0/ 0 0 0)+(0 0 0/ 0 0 0/ 0 0 1)) = (a b 0/ 0 a 0/ 0 0 a+1) et donc avec b=1 et a=2 on a aI3+bB=A
le problème c'est que j'ai trois matrices, et j'ai toujours fait des exemples avec deux matrices pour avoir (aI+bB)^n = binome de Newton...
Donc soit mon expression de départ est fausse, mais je ne vois pas comment exprimer A à l'aide de seulement deux matrices si je veux avoir l'identité à l'intérieur
Merci de m'expliquer
Binôme de Newton et Matrice
4 messages
- Page 1 sur 1
hello,
si t'écris A=M+B avec
et
alors si tu écris le binome, t'as
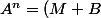^n=\bigsum_{k=0}^n C(k,n) M^kB^{n-k})
et la plupart des B^{n-k} vaudront 0, du coup il te reste plus trop de termes à calculer
il faut quand même vérifier que M et B commutent
si t'écris A=M+B avec
- Code: Tout sélectionner
M=
2 0 0
0 2 0
0 0 3
et
- Code: Tout sélectionner
B=
0 1 0
0 0 0
0 0 0
alors si tu écris le binome, t'as
et la plupart des B^{n-k} vaudront 0, du coup il te reste plus trop de termes à calculer
il faut quand même vérifier que M et B commutent
la vie est une fête 
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
