Bijectivité de x+sin(x)
14 messages
- Page 1 sur 1
Bijectivité de x+sin(x)
bonjour
on demande de montrer que pour tout x dans R, f(x)= x+sin(x) est bijective.
je propose de montrer qu'elle est d'abord injective puis surjective.
injectivité:
soit x,x' dans R
f(x) = f(x') --> x+sin(x) = x'+sin(x') --> x = x'
donc f est injective
surjectivité:
pour tout x,y dans R
on cherche x dans R tel que f(x) = y
x+sin(x) = y
comment résout-on l'équation?
on demande de montrer que pour tout x dans R, f(x)= x+sin(x) est bijective.
je propose de montrer qu'elle est d'abord injective puis surjective.
injectivité:
soit x,x' dans R
f(x) = f(x') --> x+sin(x) = x'+sin(x') --> x = x'
donc f est injective
surjectivité:
pour tout x,y dans R
on cherche x dans R tel que f(x) = y
x+sin(x) = y
comment résout-on l'équation?
Re: Bijectivité de x+sin(x)
niggito a écrit:
injectivité:
soit x,x' dans R
f(x) = f(x') --> x+sin(x) = x'+sin(x') --> x = x'
donc f est injective
bonjour
tu n'as rien démontré
Calcul plutôt f'(x)
Re: Bijectivité de x+sin(x)
Bonjour
D'abord pour l'injectivité tu n'as rien démontré. Qu'est-ce qui te permet d'affirmer que=x'+\sin(x')) entraine
entraine 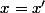 ?
?
Pour la surjectivité, tu ne pourras pas résoudre cette équation. Regarde les limites de à
à  et
et  .
.
Enfin, on ne te demande pas de montrer que est bijective pour tout
est bijective pour tout  , ce qui ne veut rien dire, mais que
, ce qui ne veut rien dire, mais que  est bijective.
est bijective.
D'abord pour l'injectivité tu n'as rien démontré. Qu'est-ce qui te permet d'affirmer que
Pour la surjectivité, tu ne pourras pas résoudre cette équation. Regarde les limites de
Enfin, on ne te demande pas de montrer que
Re: Bijectivité de x+sin(x)
merci pour l'aide,
f'(x) = 1+ cos(x)
or -1<cos(x)<1 (large)
donc f'(x) >0 (large)
donc f est croissante
sauf que pour juger de la bijectivité de f on a besoin de la stricte croissance
f'(x) = 1+ cos(x)
or -1<cos(x)<1 (large)
donc f'(x) >0 (large)
donc f est croissante
sauf que pour juger de la bijectivité de f on a besoin de la stricte croissance
Re: Bijectivité de x+sin(x)
f'(x)>=0 et l'ensemble des x tels que f'(x)=0 ne contient pas d'intervalle ouvert non vide donc f est strictement croissante
Re: Bijectivité de x+sin(x)
Non, pour avoir un changement de sens, il faut que la dérivée s'annule et qu'elle change de signe.
Re: Bijectivité de x+sin(x)
https://fr.wikiversity.org/wiki/Fonction_d%C3%A9riv%C3%A9e/D%C3%A9riv%C3%A9e_et_variations
Comme l'a dit chan79
Soit ƒ une fonction dérivable sur un intervalle I
Si pour tout>0}) sauf peut-être en un nombre fini de points où f′(x) s'annule, alors ƒ est strictement croissante sur I.
sauf peut-être en un nombre fini de points où f′(x) s'annule, alors ƒ est strictement croissante sur I.
De même, si pour tout<0}) sauf peut-être en un nombre fini de points où f′(x) s'annule, alors ƒ est strictement décroissante sur I.
sauf peut-être en un nombre fini de points où f′(x) s'annule, alors ƒ est strictement décroissante sur I.
Comme l'a dit chan79
Soit ƒ une fonction dérivable sur un intervalle I
Si pour tout
De même, si pour tout
Re: Bijectivité de x+sin(x)
Mais ici il y a une infinité de points! C'est bien parce que l'intérieur est vide, ou parce qu'il n'y a pas de changement de signe que ça marche!
Re: Bijectivité de x+sin(x)
L'ensemble des zéros de la dérivée f' forment un ensemble discret sans point d'accumulation.
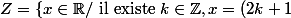\pi \})
L'intersection de Z avec un intervalle fermé,borné (un compact) est réduit à un nombre fini de points.
Sur le complémentaire, f'>0 et f est strictement croissante. En raccordant les intervalles,
f est strictement croissante sur
L'intersection de Z avec un intervalle fermé,borné (un compact) est réduit à un nombre fini de points.
Sur le complémentaire, f'>0 et f est strictement croissante. En raccordant les intervalles,
f est strictement croissante sur
Modifié en dernier par mathelot le 01 Jan 2019, 16:30, modifié 1 fois.
Re: Bijectivité de x+sin(x)
Sur un intervalle, il y a un nombre fini de points.
D'autre part, même sur IR, il n'y pas d'intervalle (non réduit à un point) où f' est nulle.
f' est nulle sur un infini "discret" de points (pas sur un intervalle de type [a,b]).
C'est ma même chose pour la fonction g(x)=x^3 dont la dérivée s'annule en x=0 mais qui est néanmoins strictement croissante sur IR.
D'autre part, même sur IR, il n'y pas d'intervalle (non réduit à un point) où f' est nulle.
f' est nulle sur un infini "discret" de points (pas sur un intervalle de type [a,b]).
C'est ma même chose pour la fonction g(x)=x^3 dont la dérivée s'annule en x=0 mais qui est néanmoins strictement croissante sur IR.
Re: Bijectivité de x+sin(x)
D'après ce qu'a mis Sa Majesté
f est strictement croissante sur tout intervalle de la forme
et tu peux ensuite conclure car deux réels a et b appartiennent forcément à un intervalle de ce type.
f est strictement croissante sur tout intervalle de la forme
et tu peux ensuite conclure car deux réels a et b appartiennent forcément à un intervalle de ce type.
Re: Bijectivité de x+sin(x)
Sa Majesté a écrit:Sur un intervalle borné, il y a un nombre fini de points.
D'autre part, même sur IR, il n'y pas d'intervalle (non réduit à un point) où f' est nulle.
f' est nulle sur un infini "discret" de points (pas sur un intervalle de type [a,b]).
.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
