Bonjour et merci d'avance
Je reprend toutes mes maths depuis le début (car je ne suis pas mathématicien) et tandis que jusque là je n'avais pas de problèmes
En fait jusqu'alors je pensais à ce problème mais je m'en foutais, à présent c'est différent
Dans mon bouquin d'algèbre, on parle d'axiomes d'une structure mais on reste vague sur ces axiomes
On sait bien que l'auteur parlera des propriétés commutativité , associativité
élément neutre , si les éléments sont régulier etc...
et il définit le fait que deux structures soient homologues
mon problème est dans le etc...
Dire dans l'absolu que deux structures sont homologues et inclure un etc... me dérange beaucoup
À défaut dans mon cahier d'algèbre je vais éliminer le mot "axiome" et m'en tenir à certaines propriétés bien définies
Voilà ci-dessous à quoi ressemble ce que dit mon bouquin ( Algèbre Lelong-Ferrand Dunod )
Définition
Deux structures sont dites homologues si 1° et 2°
1°
Elles ont les lois internes en même nombre, les lois externes en même nombre
les lois externes font intervenir les mêmes domaines d'opérateurs
mon commentaire personnel (ça me va puisque il me suffit de définir ces lois et d'en rester là)
2°
Les axiomes des deux structures sont identiques
(puis l'auteur rajoute) :
De façon précise, on peut établir entre les lois de ces deux structures,
une correspondance telle que les lois vérifient les mêmes axiomes
___________________
Mon commentaire personnel concernant le point 2°
Bah justement autant parler de ces axiomes et les nommer précisément
À la limite on pourrait parler de structures homologues par rapport aux axiomes
A1, A2,...,An
Qu'en pensez vous ?
Pensez vous que j'ai raison de me prendre la tête avec ça?
Je ne suis pas mathématicien mais je suis maniaque et quand quelque chose est flou ça me rend malade
Axiomes d'une structure
5 messages
- Page 1 sur 1
Re: Axiomes d'une structure
Bof, inutile de te prendre la tête avec ça. C'est un langage vieillot et pas très utile. Dire que deux structures sont homologues, dans le langage du bouquin, revient à dire que ces deux structures sont les modèles d'une même théorie (une théorie, c'est un langage + des axiomes qui sont des formules de ce langage).
Re: Axiomes d'une structure
Eh bien merci GaBuZoMeu
Je vais passer là-dessus et voir si les propriétés "usuelles" sont respectées (ou pas) et m'en tenir là
Je vais passer là-dessus et voir si les propriétés "usuelles" sont respectées (ou pas) et m'en tenir là
Re: Axiomes d'une structure
Bonjour et merci d'avance
ce sujet est un sujet d'algèbre (sauf qu'il est fini) ceci dit je ne trouve pas de rubrique latex sur le forum
comment écrit-on avec un gros \wedge pour l'ensemble des formes k-linéaires alternées sur E
il est trop petit le wedge là ->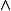
ce sujet est un sujet d'algèbre (sauf qu'il est fini) ceci dit je ne trouve pas de rubrique latex sur le forum
comment écrit-on avec un gros \wedge pour l'ensemble des formes k-linéaires alternées sur E
il est trop petit le wedge là ->
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
