Axiomes d'un espace vectoriel

[biss]

Salut. Une fois de plus j'ai du mal à m'en sortir sur un problème
On me demande de vérifier les 8 axiomes qui font de D ( une droite de R^3) un R-espace vectoriel.
D est une droite de R^3 passant par l'origine définie


Déjà j'ai fais
1) D passe par l'orgine alors
Je connais les 8 axiomes mais je ne sais pas comment les vérifier.

[zygomatique]

salut

soit M(x, y, z) et N(u, v, w) deux éléments de D

1/ que vérifie (les coordonnées de) M ?
2/ que vérifie (les coordonnées de) N ?
3/ que doit vérifier (les coordonnées de) M + N ?

...

[biss]

Les cordonnées de M vérifie


le s cordonnées de N vérifie


1) les cordonnées M+N= N+M car


2) Même chose que 1) avec (M+N)+L=M+(N+L)
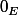
3) vérifie les 2 équations alors il est élément
4) comment montrer la symétrie des éléments ?

[zygomatique]

certes mais il faut le prouver maintenant que les coordonnées de M + N vérifient ce que tu as écrit ....

[biss]

Dans ce cas je mettrai

[Ben314]

Salut,
Juste une question qui me tarabusque :
Tu es parfaitement sûr que ce sont les axiomes d'espace vectoriel que tu es sensé vérifier ? (ça me semble très très con...)
Ca serait pas plutôt les axiome de sous-espace vectoriel que tu es sensé vérifier par hasard ?

[zygomatique]

ce que tu fais ne prouve rien ....

comment prouver 3/ en utilisant 1/ et 2/ ?

[biss]

Comme 0=0+0
ax+by+cy+au+by+cw=0
a'x+b'y+c'z+a'u+b'v+c'w=0
Équivalent a
a(x+v)+b(y+v)+z(c+w)=0
a'(x+u)+b'(y+v)+f'(z+w)=0
C'est comme ça on fait ?